A General Compressive Sensing Construct using Density Evolution
Paper and Code
Apr 11, 2022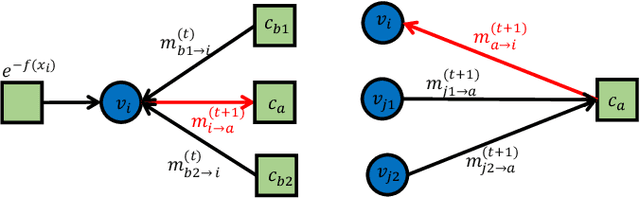
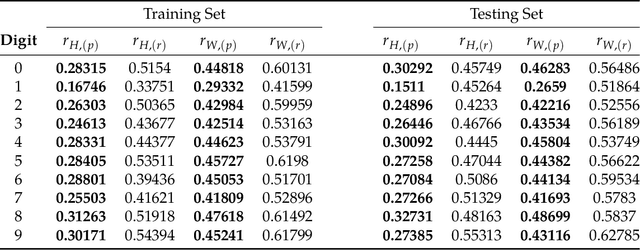

This paper proposes a general framework to design a sparse sensing matrix $\ensuremath{\mathbf{A}}\in \mathbb{R}^{m\times n}$, in a linear measurement system $\ensuremath{\mathbf{y}} = \ensuremath{\mathbf{Ax}}^{\natural} + \ensuremath{\mathbf{w}}$, where $\ensuremath{\mathbf{y}} \in \mathbb{R}^m$, $\ensuremath{\mathbf{x}}^{\natural}\in \RR^n$, and $\ensuremath{\mathbf{w}}$ denote the measurements, the signal with certain structures, and the measurement noise, respectively. By viewing the signal reconstruction from the measurements as a message passing algorithm over a graphical model, we leverage tools from coding theory in the design of low density parity check codes, namely the density evolution, and provide a framework for the design of matrix $\ensuremath{\mathbf{A}}$. Particularly, compared to the previous methods, our proposed framework enjoys the following desirable properties: ($i$) Universality: the design supports both regular sensing and preferential sensing, and incorporates them in a single framework; ($ii$) Flexibility: the framework can easily adapt the design of $\bA$ to a signal $\ensuremath{\mathbf{x}}^{\natural}$ with different underlying structures. As an illustration, we consider the $\ell_1$ regularizer, which correspond to Lasso, for both the regular sensing and preferential sensing scheme. Noteworthy, our framework can reproduce the classical result of Lasso, i.e., $m\geq c_0 k\log(n/k)$ (the regular sensing) with regular design after proper distribution approximation, where $c_0 > 0$ is some fixed constant. We also provide numerical experiments to confirm the analytical results and demonstrate the superiority of our framework whenever a preferential treatment of a sub-block of vector $\bx^{\natural}$ is required.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge