Mosaic-SDF for 3D Generative Models

Current diffusion or flow-based generative models for 3D shapes divide to two: distilling pre-trained 2D image diffusion models, and training directly on 3D shapes. When training a diffusion or flow models on 3D shapes a crucial design choice is the shape representation. An effective shape representation needs to adhere three design principles: it should allow an efficient conversion of large 3D datasets to the representation form; it should provide a good tradeoff of approximation power versus number of parameters; and it should have a simple tensorial form that is compatible with existing powerful neural architectures. While standard 3D shape representations such as volumetric grids and point clouds do not adhere to all these principles simultaneously, we advocate in this paper a new representation that does. We introduce Mosaic-SDF (M-SDF): a simple 3D shape representation that approximates the Signed Distance Function (SDF) of a given shape by using a set of local grids spread near the shape's boundary. The M-SDF representation is fast to compute for each shape individually making it readily parallelizable; it is parameter efficient as it only covers the space around the shape's boundary; and it has a simple matrix form, compatible with Transformer-based architectures. We demonstrate the efficacy of the M-SDF representation by using it to train a 3D generative flow model including class-conditioned generation with the 3D Warehouse dataset, and text-to-3D generation using a dataset of about 600k caption-shape pairs.

VisCo Grids: Surface Reconstruction with Viscosity and Coarea Grids

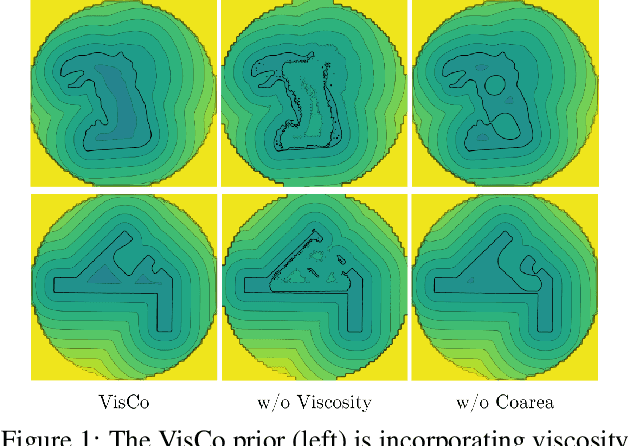
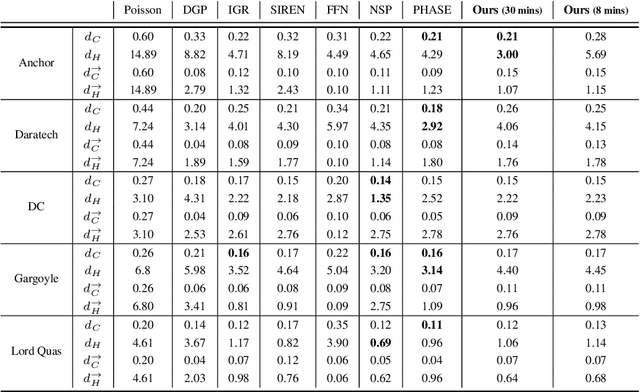
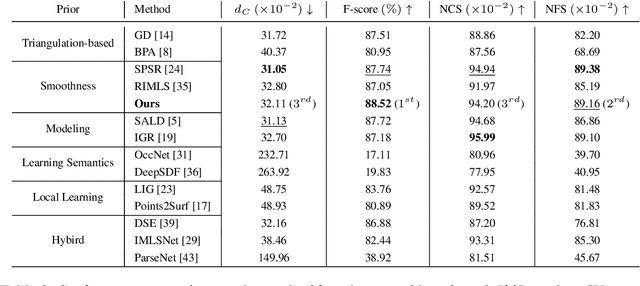
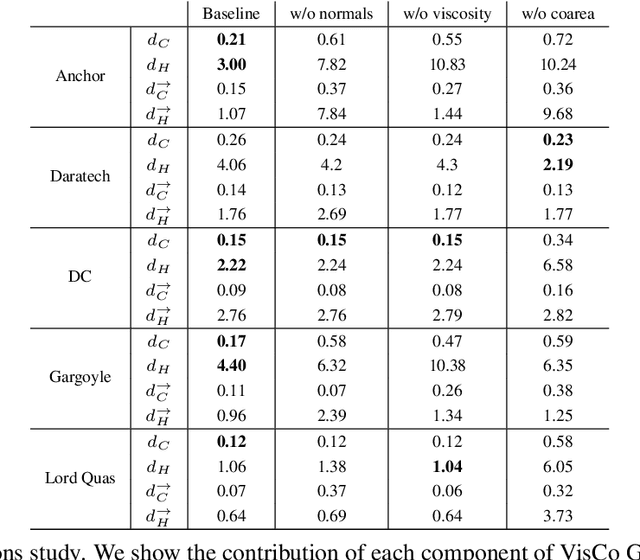
Surface reconstruction has been seeing a lot of progress lately by utilizing Implicit Neural Representations (INRs). Despite their success, INRs often introduce hard to control inductive bias (i.e., the solution surface can exhibit unexplainable behaviours), have costly inference, and are slow to train. The goal of this work is to show that replacing neural networks with simple grid functions, along with two novel geometric priors achieve comparable results to INRs, with instant inference, and improved training times. To that end we introduce VisCo Grids: a grid-based surface reconstruction method incorporating Viscosity and Coarea priors. Intuitively, the Viscosity prior replaces the smoothness inductive bias of INRs, while the Coarea favors a minimal area solution. Experimenting with VisCo Grids on a standard reconstruction baseline provided comparable results to the best performing INRs on this dataset.

BakedSDF: Meshing Neural SDFs for Real-Time View Synthesis

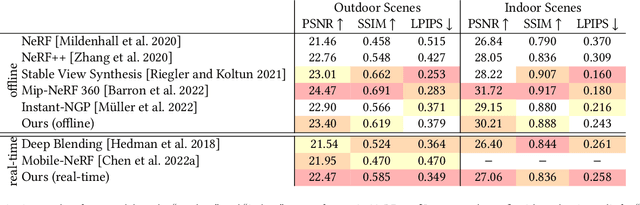
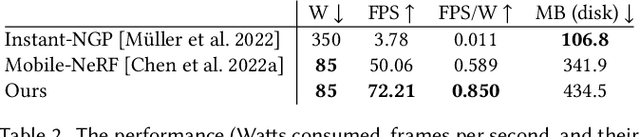
We present a method for reconstructing high-quality meshes of large unbounded real-world scenes suitable for photorealistic novel view synthesis. We first optimize a hybrid neural volume-surface scene representation designed to have well-behaved level sets that correspond to surfaces in the scene. We then bake this representation into a high-quality triangle mesh, which we equip with a simple and fast view-dependent appearance model based on spherical Gaussians. Finally, we optimize this baked representation to best reproduce the captured viewpoints, resulting in a model that can leverage accelerated polygon rasterization pipelines for real-time view synthesis on commodity hardware. Our approach outperforms previous scene representations for real-time rendering in terms of accuracy, speed, and power consumption, and produces high quality meshes that enable applications such as appearance editing and physical simulation.

MultiDiffusion: Fusing Diffusion Paths for Controlled Image Generation

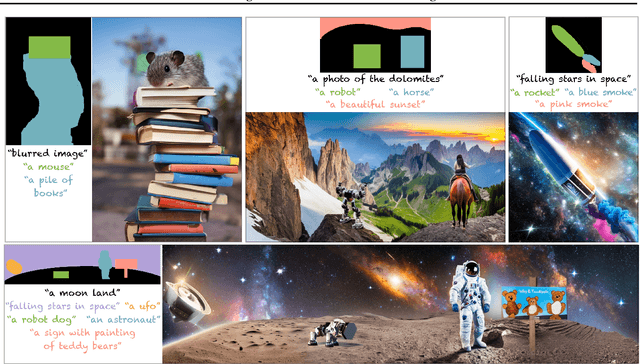
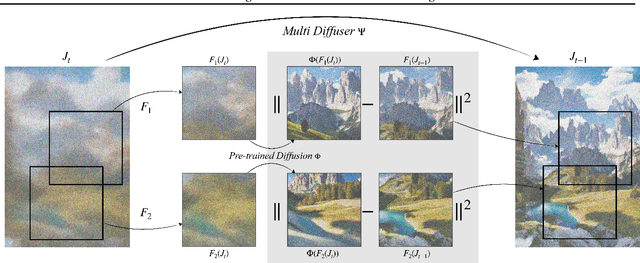
Recent advances in text-to-image generation with diffusion models present transformative capabilities in image quality. However, user controllability of the generated image, and fast adaptation to new tasks still remains an open challenge, currently mostly addressed by costly and long re-training and fine-tuning or ad-hoc adaptations to specific image generation tasks. In this work, we present MultiDiffusion, a unified framework that enables versatile and controllable image generation, using a pre-trained text-to-image diffusion model, without any further training or finetuning. At the center of our approach is a new generation process, based on an optimization task that binds together multiple diffusion generation processes with a shared set of parameters or constraints. We show that MultiDiffusion can be readily applied to generate high quality and diverse images that adhere to user-provided controls, such as desired aspect ratio (e.g., panorama), and spatial guiding signals, ranging from tight segmentation masks to bounding boxes. Project webpage: https://multidiffusion.github.io

Volume Rendering of Neural Implicit Surfaces

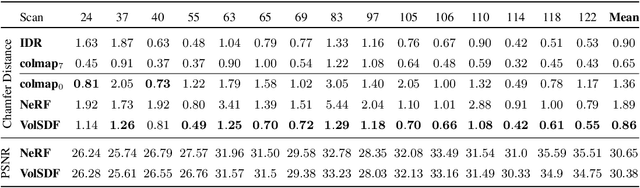
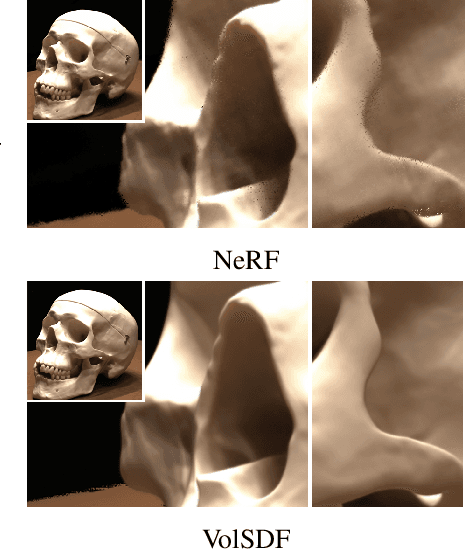
Neural volume rendering became increasingly popular recently due to its success in synthesizing novel views of a scene from a sparse set of input images. So far, the geometry learned by neural volume rendering techniques was modeled using a generic density function. Furthermore, the geometry itself was extracted using an arbitrary level set of the density function leading to a noisy, often low fidelity reconstruction. The goal of this paper is to improve geometry representation and reconstruction in neural volume rendering. We achieve that by modeling the volume density as a function of the geometry. This is in contrast to previous work modeling the geometry as a function of the volume density. In more detail, we define the volume density function as Laplace's cumulative distribution function (CDF) applied to a signed distance function (SDF) representation. This simple density representation has three benefits: (i) it provides a useful inductive bias to the geometry learned in the neural volume rendering process; (ii) it facilitates a bound on the opacity approximation error, leading to an accurate sampling of the viewing ray. Accurate sampling is important to provide a precise coupling of geometry and radiance; and (iii) it allows efficient unsupervised disentanglement of shape and appearance in volume rendering. Applying this new density representation to challenging scene multiview datasets produced high quality geometry reconstructions, outperforming relevant baselines. Furthermore, switching shape and appearance between scenes is possible due to the disentanglement of the two.

Universal Differentiable Renderer for Implicit Neural Representations

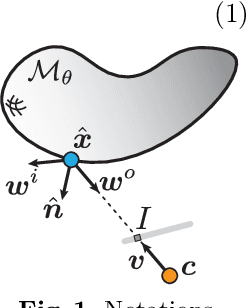
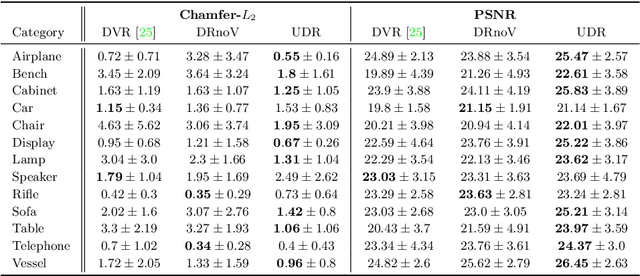
The goal of this work is to learn implicit 3D shape representation with 2D supervision (i.e., a collection of images). To that end we introduce the Universal Differentiable Renderer (UDR) a neural network architecture that can provably approximate reflected light from an implicit neural representation of a 3D surface, under a wide set of reflectance properties and lighting conditions. Experimenting with the task of multiview 3D reconstruction, we find our model to improve upon the baselines in the accuracy of the reconstructed 3D geometry and rendering from unseen viewing directions.

Implicit Geometric Regularization for Learning Shapes

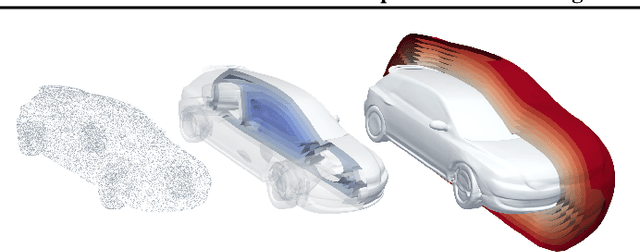
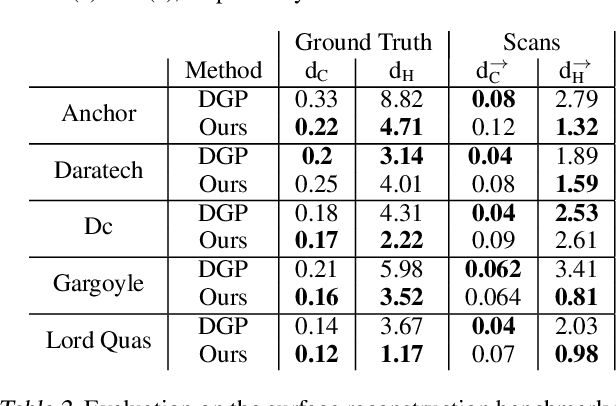
Representing shapes as level sets of neural networks has been recently proved to be useful for different shape analysis and reconstruction tasks So far, such representations were computed using either: (i) pre-computed implicit shape representations; or (ii) loss functions explicitly defined over the neural level sets. In this paper we offer a new paradigm for computing high fidelity implicit neural representations directly from raw data (i.e., point clouds, with or without normal information). We observe that a rather simple loss function, encouraging the neural network to vanish on the input point cloud and to have a unit norm gradient, possesses an implicit geometric regularization property that favors smooth and natural zero level set surfaces, avoiding bad zero-loss solutions. We provide a theoretical analysis of this property for the linear case, and show that, in practice, our method leads to state of the art implicit neural representations with higher level-of-details and fidelity compared to previous methods.

Controlling Neural Level Sets

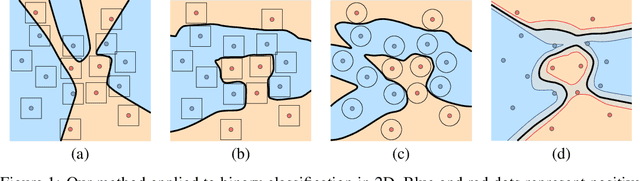
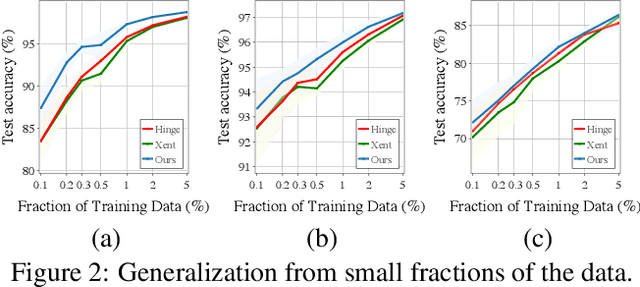
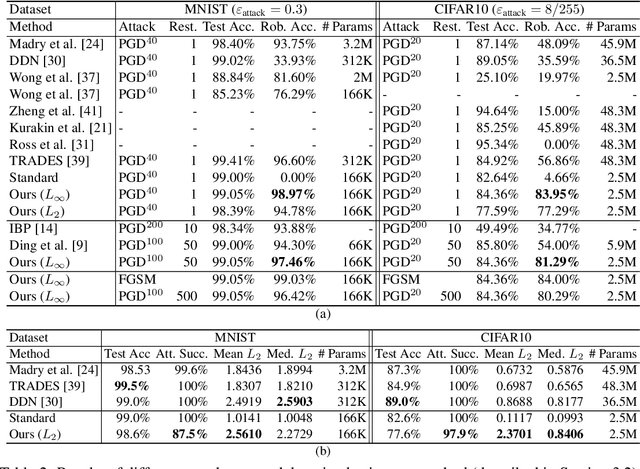
The level sets of neural networks represent fundamental properties such as decision boundaries of classifiers and are used to model non-linear manifold data such as curves and surfaces. Thus, methods for controlling the neural level sets could find many applications in machine learning. In this paper we present a simple and scalable approach to directly control level sets of a deep neural network. Our method consists of two parts: (i) sampling of the neural level sets, and (ii) relating the samples' positions to the network parameters. The latter is achieved by a \emph{sample network} that is constructed by adding a single fixed linear layer to the original network. In turn, the sample network can be used to incorporate the level set samples into a loss function of interest. We have tested our method on three different learning tasks: training networks robust to adversarial attacks, improving generalization to unseen data, and curve and surface reconstruction from point clouds. Notably, we increase robust accuracy to the level of standard classification accuracy in off-the-shelf networks, improving it by 2\% in MNIST and 27\% in CIFAR10 compared to state-of-the-art methods. For surface reconstruction, we produce high fidelity surfaces directly from raw 3D point clouds.