ReMatching Dynamic Reconstruction Flow

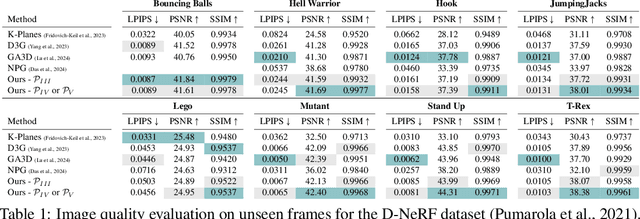
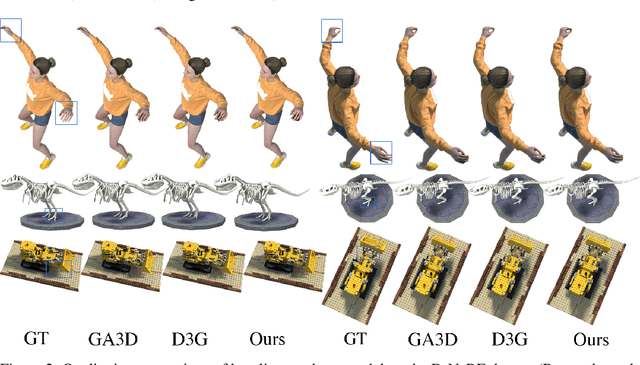
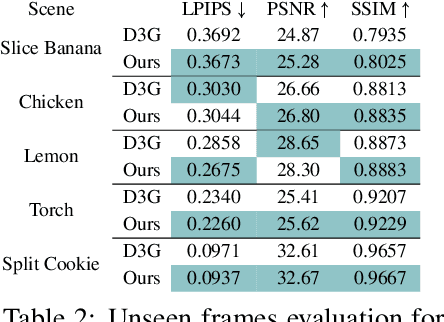
Reconstructing dynamic scenes from image inputs is a fundamental computer vision task with many downstream applications. Despite recent advancements, existing approaches still struggle to achieve high-quality reconstructions from unseen viewpoints and timestamps. This work introduces the ReMatching framework, designed to improve generalization quality by incorporating deformation priors into dynamic reconstruction models. Our approach advocates for velocity-field-based priors, for which we suggest a matching procedure that can seamlessly supplement existing dynamic reconstruction pipelines. The framework is highly adaptable and can be applied to various dynamic representations. Moreover, it supports integrating multiple types of model priors and enables combining simpler ones to create more complex classes. Our evaluations on popular benchmarks involving both synthetic and real-world dynamic scenes demonstrate a clear improvement in reconstruction accuracy of current state-of-the-art models.

SpaceMesh: A Continuous Representation for Learning Manifold Surface Meshes

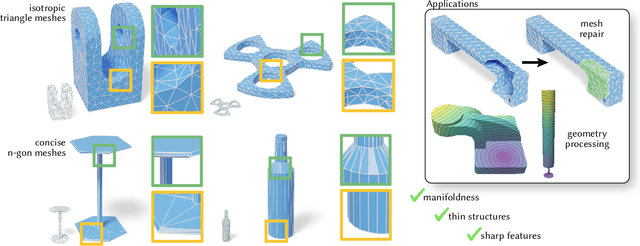
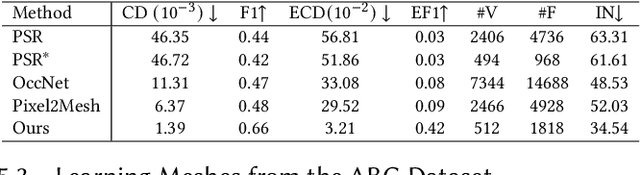
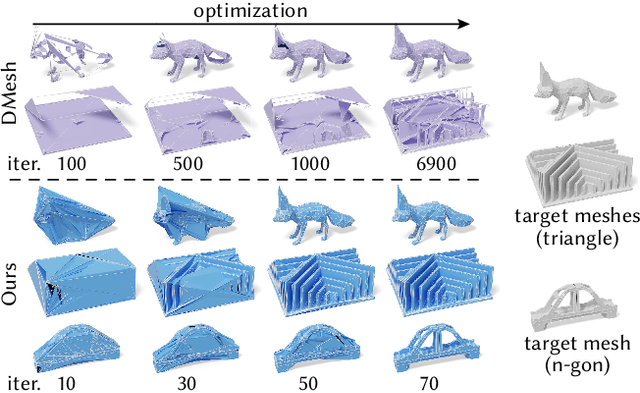
Meshes are ubiquitous in visual computing and simulation, yet most existing machine learning techniques represent meshes only indirectly, e.g. as the level set of a scalar field or deformation of a template, or as a disordered triangle soup lacking local structure. This work presents a scheme to directly generate manifold, polygonal meshes of complex connectivity as the output of a neural network. Our key innovation is to define a continuous latent connectivity space at each mesh vertex, which implies the discrete mesh. In particular, our vertex embeddings generate cyclic neighbor relationships in a halfedge mesh representation, which gives a guarantee of edge-manifoldness and the ability to represent general polygonal meshes. This representation is well-suited to machine learning and stochastic optimization, without restriction on connectivity or topology. We first explore the basic properties of this representation, then use it to fit distributions of meshes from large datasets. The resulting models generate diverse meshes with tessellation structure learned from the dataset population, with concise details and high-quality mesh elements. In applications, this approach not only yields high-quality outputs from generative models, but also enables directly learning challenging geometry processing tasks such as mesh repair.

Approximately Piecewise E(3) Equivariant Point Networks

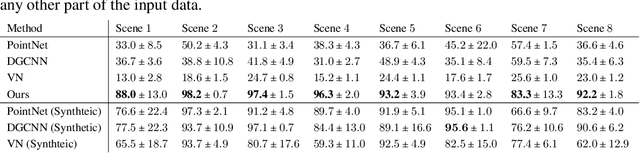
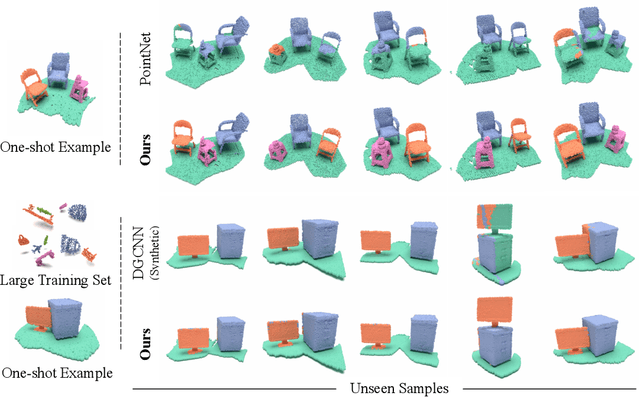
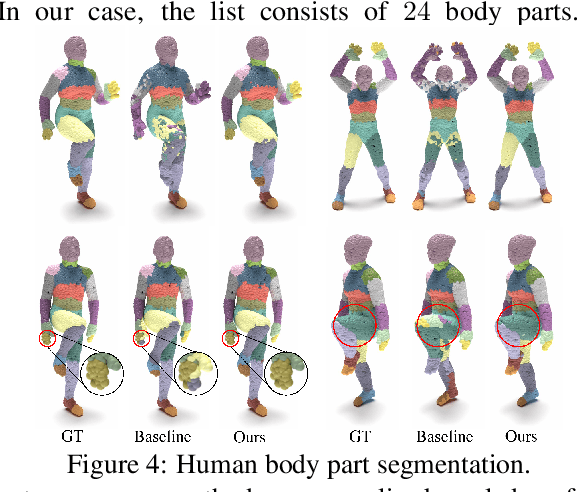
Integrating a notion of symmetry into point cloud neural networks is a provably effective way to improve their generalization capability. Of particular interest are $E(3)$ equivariant point cloud networks where Euclidean transformations applied to the inputs are preserved in the outputs. Recent efforts aim to extend networks that are $E(3)$ equivariant, to accommodate inputs made of multiple parts, each of which exhibits local $E(3)$ symmetry. In practical settings, however, the partitioning into individually transforming regions is unknown a priori. Errors in the partition prediction would unavoidably map to errors in respecting the true input symmetry. Past works have proposed different ways to predict the partition, which may exhibit uncontrolled errors in their ability to maintain equivariance to the actual partition. To this end, we introduce APEN: a general framework for constructing approximate piecewise-$E(3)$ equivariant point networks. Our primary insight is that functions that are equivariant with respect to a finer partition will also maintain equivariance in relation to the true partition. Leveraging this observation, we propose a design where the equivariance approximation error at each layers can be bounded solely in terms of (i) uncertainty quantification of the partition prediction, and (ii) bounds on the probability of failing to suggest a proper subpartition of the ground truth one. We demonstrate the effectiveness of APEN using two data types exemplifying part-based symmetry: (i) real-world scans of room scenes containing multiple furniture-type objects; and, (ii) human motions, characterized by articulated parts exhibiting rigid movement. Our empirical results demonstrate the advantage of integrating piecewise $E(3)$ symmetry into network design, showing a distinct improvement in generalization compared to prior works for both classification and segmentation tasks.

Neural Kernel Surface Reconstruction

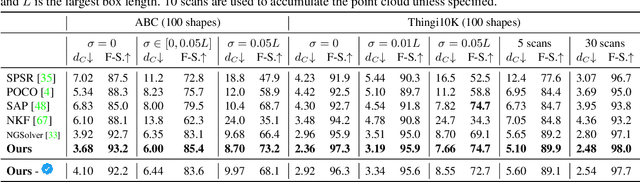
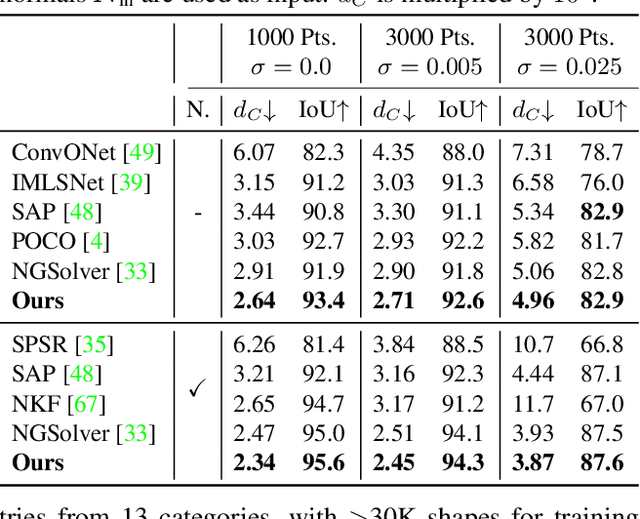
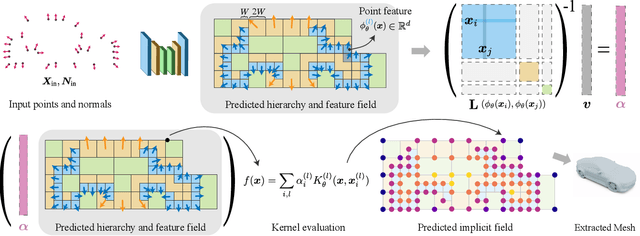
We present a novel method for reconstructing a 3D implicit surface from a large-scale, sparse, and noisy point cloud. Our approach builds upon the recently introduced Neural Kernel Fields (NKF) representation. It enjoys similar generalization capabilities to NKF, while simultaneously addressing its main limitations: (a) We can scale to large scenes through compactly supported kernel functions, which enable the use of memory-efficient sparse linear solvers. (b) We are robust to noise, through a gradient fitting solve. (c) We minimize training requirements, enabling us to learn from any dataset of dense oriented points, and even mix training data consisting of objects and scenes at different scales. Our method is capable of reconstructing millions of points in a few seconds, and handling very large scenes in an out-of-core fashion. We achieve state-of-the-art results on reconstruction benchmarks consisting of single objects, indoor scenes, and outdoor scenes.

Frame Averaging for Equivariant Shape Space Learning

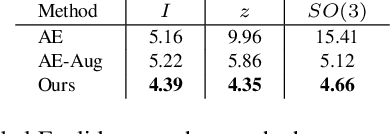
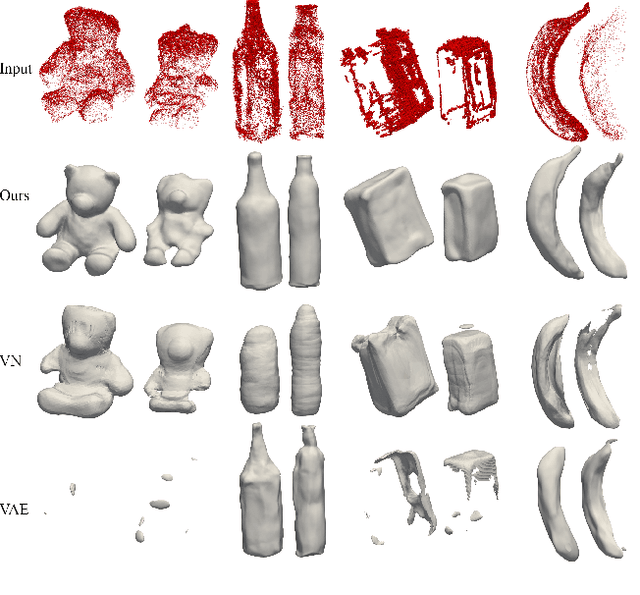
The task of shape space learning involves mapping a train set of shapes to and from a latent representation space with good generalization properties. Often, real-world collections of shapes have symmetries, which can be defined as transformations that do not change the essence of the shape. A natural way to incorporate symmetries in shape space learning is to ask that the mapping to the shape space (encoder) and mapping from the shape space (decoder) are equivariant to the relevant symmetries. In this paper, we present a framework for incorporating equivariance in encoders and decoders by introducing two contributions: (i) adapting the recent Frame Averaging (FA) framework for building generic, efficient, and maximally expressive Equivariant autoencoders; and (ii) constructing autoencoders equivariant to piecewise Euclidean motions applied to different parts of the shape. To the best of our knowledge, this is the first fully piecewise Euclidean equivariant autoencoder construction. Training our framework is simple: it uses standard reconstruction losses and does not require the introduction of new losses. Our architectures are built of standard (backbone) architectures with the appropriate frame averaging to make them equivariant. Testing our framework on both rigid shapes dataset using implicit neural representations, and articulated shape datasets using mesh-based neural networks show state-of-the-art generalization to unseen test shapes, improving relevant baselines by a large margin. In particular, our method demonstrates significant improvement in generalizing to unseen articulated poses.

Frame Averaging for Invariant and Equivariant Network Design

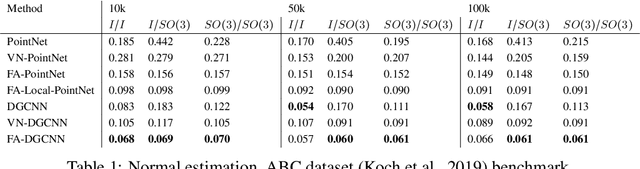
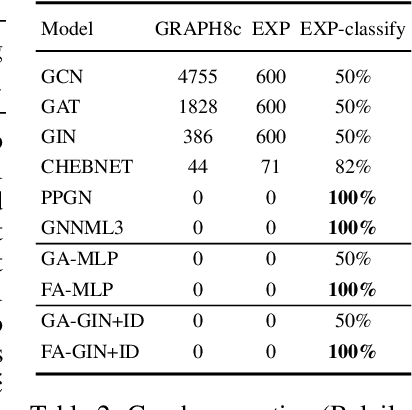
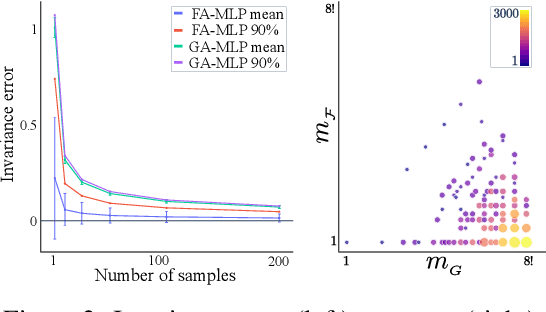
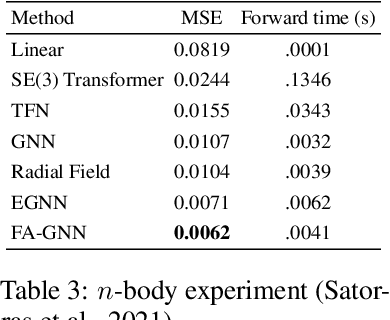
Many machine learning tasks involve learning functions that are known to be invariant or equivariant to certain symmetries of the input data. However, it is often challenging to design neural network architectures that respect these symmetries while being expressive and computationally efficient. For example, Euclidean motion invariant/equivariant graph or point cloud neural networks. We introduce Frame Averaging (FA), a general purpose and systematic framework for adapting known (backbone) architectures to become invariant or equivariant to new symmetry types. Our framework builds on the well known group averaging operator that guarantees invariance or equivariance but is intractable. In contrast, we observe that for many important classes of symmetries, this operator can be replaced with an averaging operator over a small subset of the group elements, called a frame. We show that averaging over a frame guarantees exact invariance or equivariance while often being much simpler to compute than averaging over the entire group. Furthermore, we prove that FA-based models have maximal expressive power in a broad setting and in general preserve the expressive power of their backbone architectures. Using frame averaging, we propose a new class of universal Graph Neural Networks (GNNs), universal Euclidean motion invariant point cloud networks, and Euclidean motion invariant Message Passing (MP) GNNs. We demonstrate the practical effectiveness of FA on several applications including point cloud normal estimation, beyond $2$-WL graph separation, and $n$-body dynamics prediction, achieving state-of-the-art results in all of these benchmarks.

Augmenting Implicit Neural Shape Representations with Explicit Deformation Fields

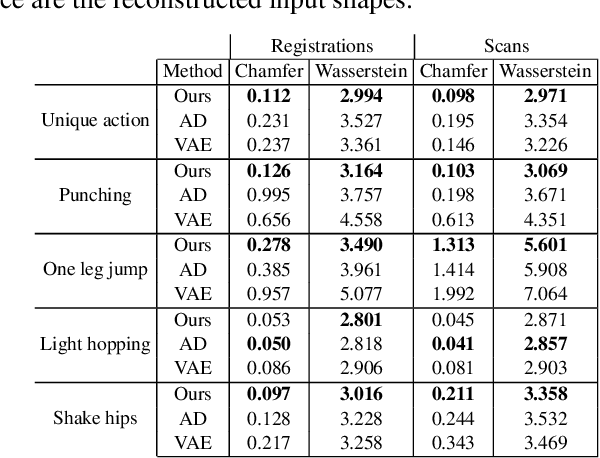
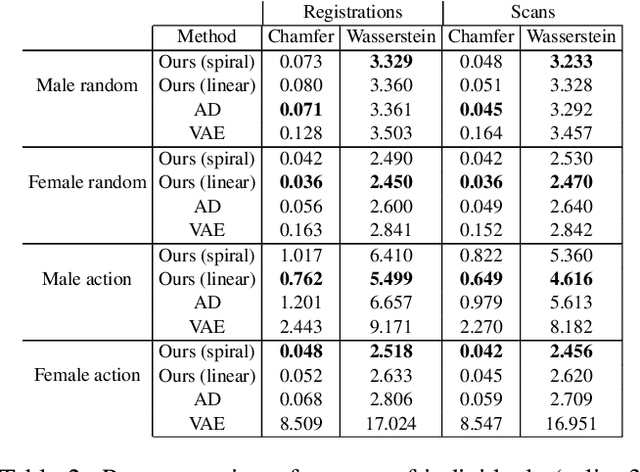
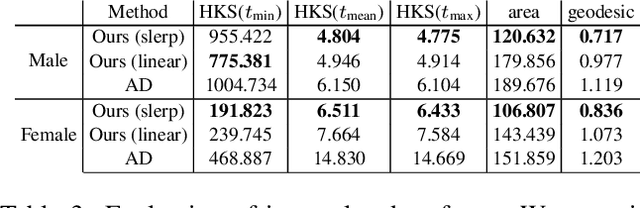
Implicit neural representation is a recent approach to learn shape collections as zero level-sets of neural networks, where each shape is represented by a latent code. So far, the focus has been shape reconstruction, while shape generalization was mostly left to generic encoder-decoder or auto-decoder regularization. In this paper we advocate deformation-aware regularization for implicit neural representations, aiming at producing plausible deformations as latent code changes. The challenge is that implicit representations do not capture correspondences between different shapes, which makes it difficult to represent and regularize their deformations. Thus, we propose to pair the implicit representation of the shapes with an explicit, piecewise linear deformation field, learned as an auxiliary function. We demonstrate that, by regularizing these deformation fields, we can encourage the implicit neural representation to induce natural deformations in the learned shape space, such as as-rigid-as-possible deformations.

Isometric Autoencoders

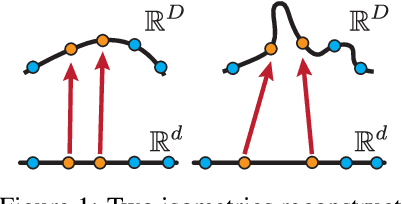
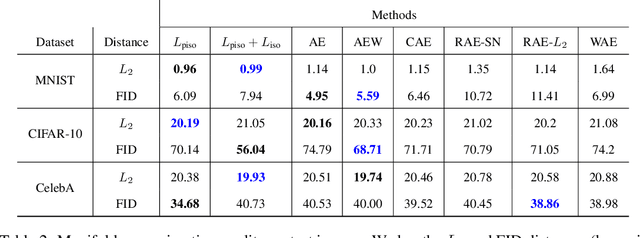
High dimensional data is often assumed to be concentrated near a low-dimensional manifold. Autoencoders (AE) is a popular technique to learn representations of such data by pushing it through a neural network with a low dimension bottleneck while minimizing a reconstruction error. Using high capacity AE often leads to a large collection of minimizers, many of which represent a low dimensional manifold that fits the data well but generalizes poorly. Two sources of bad generalization are: extrinsic, where the learned manifold possesses extraneous parts that are far from the data; and intrinsic, where the encoder and decoder introduce arbitrary distortion in the low dimensional parameterization. An approach taken to alleviate these issues is to add a regularizer that favors a particular solution; common regularizers promote sparsity, small derivatives, or robustness to noise. In this paper, we advocate an isometry (ie, distance preserving) regularizer. Specifically, our regularizer encourages: (i) the decoder to be an isometry; and (ii) the encoder to be a pseudo-isometry, where pseudo-isometry is an extension of an isometry with an orthogonal projection operator. In a nutshell, (i) preserves all geometric properties of the data such as volume, length, angle, and probability density. It fixes the intrinsic degree of freedom since any two isometric decoders to the same manifold will differ by a rigid motion. (ii) Addresses the extrinsic degree of freedom by minimizing derivatives in orthogonal directions to the manifold and hence disfavoring complicated manifold solutions. Experimenting with the isometry regularizer on dimensionality reduction tasks produces useful low-dimensional data representations, while incorporating it in AE models leads to an improved generalization.

SAL++: Sign Agnostic Learning with Derivatives

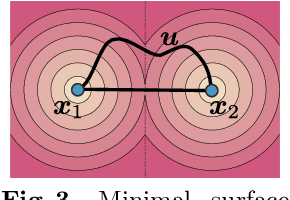
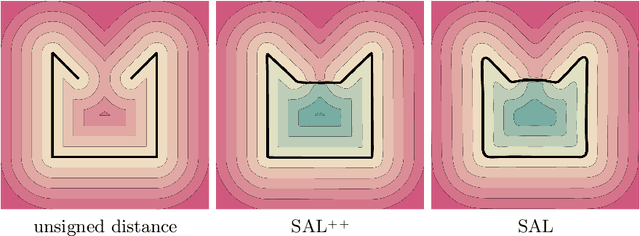
Learning 3D geometry directly from raw data, such as point clouds, triangle soups, or un-oriented meshes is still a challenging task that feeds many downstream computer vision and graphics applications. In this paper, we introduce SAL++: a method for learning implicit neural representations of shapes directly from such raw data. We build upon the recent sign agnostic learning (SAL) approach and generalize it to include derivative data in a sign agnostic manner. In more detail, given the unsigned distance function to the input raw data, we suggest a novel sign agnostic regression loss, incorporating both pointwise values and gradients of the unsigned distance function. Optimizing this loss leads to a signed implicit function solution, the zero level set of which is a high quality, valid manifold approximation to the input 3D data. We demonstrate the efficacy of SAL++ shape space learning from two challenging datasets: ShapeNet that contains inconsistent orientation and non-manifold meshes, and D-Faust that contains raw 3D scans (triangle soups). On both these datasets, we present state-of-the-art results.

Universal Differentiable Renderer for Implicit Neural Representations

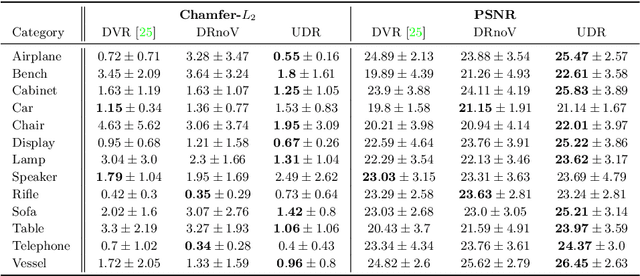
The goal of this work is to learn implicit 3D shape representation with 2D supervision (i.e., a collection of images). To that end we introduce the Universal Differentiable Renderer (UDR) a neural network architecture that can provably approximate reflected light from an implicit neural representation of a 3D surface, under a wide set of reflectance properties and lighting conditions. Experimenting with the task of multiview 3D reconstruction, we find our model to improve upon the baselines in the accuracy of the reconstructed 3D geometry and rendering from unseen viewing directions.