SAL++: Sign Agnostic Learning with Derivatives

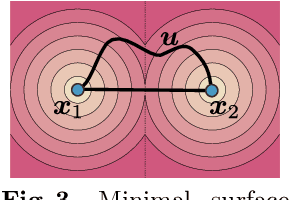
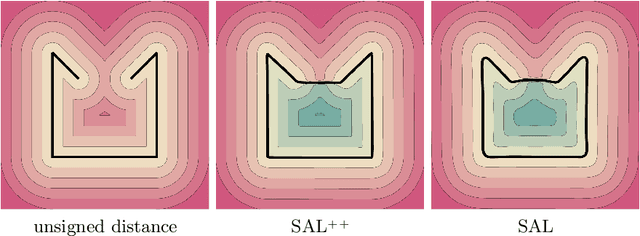
Learning 3D geometry directly from raw data, such as point clouds, triangle soups, or un-oriented meshes is still a challenging task that feeds many downstream computer vision and graphics applications. In this paper, we introduce SAL++: a method for learning implicit neural representations of shapes directly from such raw data. We build upon the recent sign agnostic learning (SAL) approach and generalize it to include derivative data in a sign agnostic manner. In more detail, given the unsigned distance function to the input raw data, we suggest a novel sign agnostic regression loss, incorporating both pointwise values and gradients of the unsigned distance function. Optimizing this loss leads to a signed implicit function solution, the zero level set of which is a high quality, valid manifold approximation to the input 3D data. We demonstrate the efficacy of SAL++ shape space learning from two challenging datasets: ShapeNet that contains inconsistent orientation and non-manifold meshes, and D-Faust that contains raw 3D scans (triangle soups). On both these datasets, we present state-of-the-art results.