PARTFIELD: Learning 3D Feature Fields for Part Segmentation and Beyond

We propose PartField, a feedforward approach for learning part-based 3D features, which captures the general concept of parts and their hierarchy without relying on predefined templates or text-based names, and can be applied to open-world 3D shapes across various modalities. PartField requires only a 3D feedforward pass at inference time, significantly improving runtime and robustness compared to prior approaches. Our model is trained by distilling 2D and 3D part proposals from a mix of labeled datasets and image segmentations on large unsupervised datasets, via a contrastive learning formulation. It produces a continuous feature field which can be clustered to yield a hierarchical part decomposition. Comparisons show that PartField is up to 20% more accurate and often orders of magnitude faster than other recent class-agnostic part-segmentation methods. Beyond single-shape part decomposition, consistency in the learned field emerges across shapes, enabling tasks such as co-segmentation and correspondence, which we demonstrate in several applications of these general-purpose, hierarchical, and consistent 3D feature fields. Check our Webpage! https://research.nvidia.com/labs/toronto-ai/partfield-release/

Neurally Integrated Finite Elements for Differentiable Elasticity on Evolving Domains

We present an elastic simulator for domains defined as evolving implicit functions, which is efficient, robust, and differentiable with respect to both shape and material. This simulator is motivated by applications in 3D reconstruction: it is increasingly effective to recover geometry from observed images as implicit functions, but physical applications require accurately simulating and optimizing-for the behavior of such shapes under deformation, which has remained challenging. Our key technical innovation is to train a small neural network to fit quadrature points for robust numerical integration on implicit grid cells. When coupled with a Mixed Finite Element formulation, this yields a smooth, fully differentiable simulation model connecting the evolution of the underlying implicit surface to its elastic response. We demonstrate the efficacy of our approach on forward simulation of implicits, direct simulation of 3D shapes during editing, and novel physics-based shape and topology optimizations in conjunction with differentiable rendering.

SpaceMesh: A Continuous Representation for Learning Manifold Surface Meshes

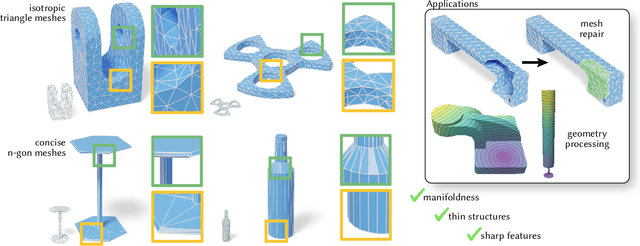
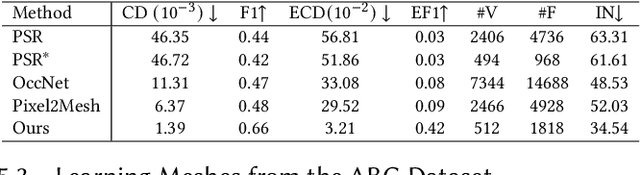
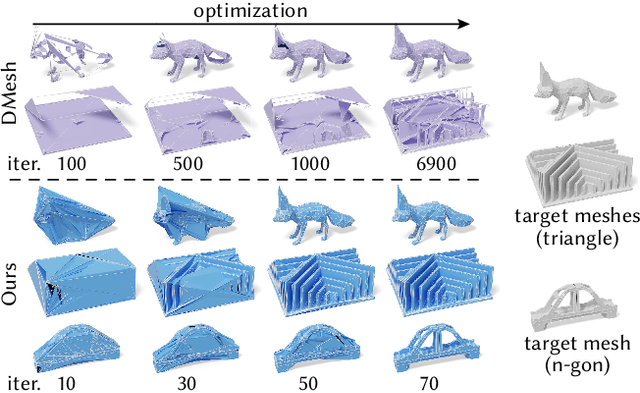
Meshes are ubiquitous in visual computing and simulation, yet most existing machine learning techniques represent meshes only indirectly, e.g. as the level set of a scalar field or deformation of a template, or as a disordered triangle soup lacking local structure. This work presents a scheme to directly generate manifold, polygonal meshes of complex connectivity as the output of a neural network. Our key innovation is to define a continuous latent connectivity space at each mesh vertex, which implies the discrete mesh. In particular, our vertex embeddings generate cyclic neighbor relationships in a halfedge mesh representation, which gives a guarantee of edge-manifoldness and the ability to represent general polygonal meshes. This representation is well-suited to machine learning and stochastic optimization, without restriction on connectivity or topology. We first explore the basic properties of this representation, then use it to fit distributions of meshes from large datasets. The resulting models generate diverse meshes with tessellation structure learned from the dataset population, with concise details and high-quality mesh elements. In applications, this approach not only yields high-quality outputs from generative models, but also enables directly learning challenging geometry processing tasks such as mesh repair.

3D Gaussian Ray Tracing: Fast Tracing of Particle Scenes

Particle-based representations of radiance fields such as 3D Gaussian Splatting have found great success for reconstructing and re-rendering of complex scenes. Most existing methods render particles via rasterization, projecting them to screen space tiles for processing in a sorted order. This work instead considers ray tracing the particles, building a bounding volume hierarchy and casting a ray for each pixel using high-performance GPU ray tracing hardware. To efficiently handle large numbers of semi-transparent particles, we describe a specialized rendering algorithm which encapsulates particles with bounding meshes to leverage fast ray-triangle intersections, and shades batches of intersections in depth-order. The benefits of ray tracing are well-known in computer graphics: processing incoherent rays for secondary lighting effects such as shadows and reflections, rendering from highly-distorted cameras common in robotics, stochastically sampling rays, and more. With our renderer, this flexibility comes at little cost compared to rasterization. Experiments demonstrate the speed and accuracy of our approach, as well as several applications in computer graphics and vision. We further propose related improvements to the basic Gaussian representation, including a simple use of generalized kernel functions which significantly reduces particle hit counts.

Adaptive Shells for Efficient Neural Radiance Field Rendering

Neural radiance fields achieve unprecedented quality for novel view synthesis, but their volumetric formulation remains expensive, requiring a huge number of samples to render high-resolution images. Volumetric encodings are essential to represent fuzzy geometry such as foliage and hair, and they are well-suited for stochastic optimization. Yet, many scenes ultimately consist largely of solid surfaces which can be accurately rendered by a single sample per pixel. Based on this insight, we propose a neural radiance formulation that smoothly transitions between volumetric- and surface-based rendering, greatly accelerating rendering speed and even improving visual fidelity. Our method constructs an explicit mesh envelope which spatially bounds a neural volumetric representation. In solid regions, the envelope nearly converges to a surface and can often be rendered with a single sample. To this end, we generalize the NeuS formulation with a learned spatially-varying kernel size which encodes the spread of the density, fitting a wide kernel to volume-like regions and a tight kernel to surface-like regions. We then extract an explicit mesh of a narrow band around the surface, with width determined by the kernel size, and fine-tune the radiance field within this band. At inference time, we cast rays against the mesh and evaluate the radiance field only within the enclosed region, greatly reducing the number of samples required. Experiments show that our approach enables efficient rendering at very high fidelity. We also demonstrate that the extracted envelope enables downstream applications such as animation and simulation.

TexFusion: Synthesizing 3D Textures with Text-Guided Image Diffusion Models

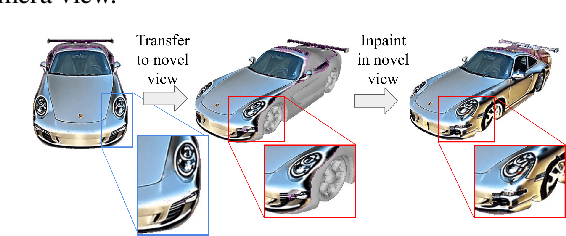
We present TexFusion (Texture Diffusion), a new method to synthesize textures for given 3D geometries, using large-scale text-guided image diffusion models. In contrast to recent works that leverage 2D text-to-image diffusion models to distill 3D objects using a slow and fragile optimization process, TexFusion introduces a new 3D-consistent generation technique specifically designed for texture synthesis that employs regular diffusion model sampling on different 2D rendered views. Specifically, we leverage latent diffusion models, apply the diffusion model's denoiser on a set of 2D renders of the 3D object, and aggregate the different denoising predictions on a shared latent texture map. Final output RGB textures are produced by optimizing an intermediate neural color field on the decodings of 2D renders of the latent texture. We thoroughly validate TexFusion and show that we can efficiently generate diverse, high quality and globally coherent textures. We achieve state-of-the-art text-guided texture synthesis performance using only image diffusion models, while avoiding the pitfalls of previous distillation-based methods. The text-conditioning offers detailed control and we also do not rely on any ground truth 3D textures for training. This makes our method versatile and applicable to a broad range of geometry and texture types. We hope that TexFusion will advance AI-based texturing of 3D assets for applications in virtual reality, game design, simulation, and more.

Flexible Isosurface Extraction for Gradient-Based Mesh Optimization

This work considers gradient-based mesh optimization, where we iteratively optimize for a 3D surface mesh by representing it as the isosurface of a scalar field, an increasingly common paradigm in applications including photogrammetry, generative modeling, and inverse physics. Existing implementations adapt classic isosurface extraction algorithms like Marching Cubes or Dual Contouring; these techniques were designed to extract meshes from fixed, known fields, and in the optimization setting they lack the degrees of freedom to represent high-quality feature-preserving meshes, or suffer from numerical instabilities. We introduce FlexiCubes, an isosurface representation specifically designed for optimizing an unknown mesh with respect to geometric, visual, or even physical objectives. Our main insight is to introduce additional carefully-chosen parameters into the representation, which allow local flexible adjustments to the extracted mesh geometry and connectivity. These parameters are updated along with the underlying scalar field via automatic differentiation when optimizing for a downstream task. We base our extraction scheme on Dual Marching Cubes for improved topological properties, and present extensions to optionally generate tetrahedral and hierarchically-adaptive meshes. Extensive experiments validate FlexiCubes on both synthetic benchmarks and real-world applications, showing that it offers significant improvements in mesh quality and geometric fidelity.

ATT3D: Amortized Text-to-3D Object Synthesis

Text-to-3D modelling has seen exciting progress by combining generative text-to-image models with image-to-3D methods like Neural Radiance Fields. DreamFusion recently achieved high-quality results but requires a lengthy, per-prompt optimization to create 3D objects. To address this, we amortize optimization over text prompts by training on many prompts simultaneously with a unified model, instead of separately. With this, we share computation across a prompt set, training in less time than per-prompt optimization. Our framework - Amortized text-to-3D (ATT3D) - enables knowledge-sharing between prompts to generalize to unseen setups and smooth interpolations between text for novel assets and simple animations.

Data-Free Learning of Reduced-Order Kinematics

Physical systems ranging from elastic bodies to kinematic linkages are defined on high-dimensional configuration spaces, yet their typical low-energy configurations are concentrated on much lower-dimensional subspaces. This work addresses the challenge of identifying such subspaces automatically: given as input an energy function for a high-dimensional system, we produce a low-dimensional map whose image parameterizes a diverse yet low-energy submanifold of configurations. The only additional input needed is a single seed configuration for the system to initialize our procedure; no dataset of trajectories is required. We represent subspaces as neural networks that map a low-dimensional latent vector to the full configuration space, and propose a training scheme to fit network parameters to any system of interest. This formulation is effective across a very general range of physical systems; our experiments demonstrate not only nonlinear and very low-dimensional elastic body and cloth subspaces, but also more general systems like colliding rigid bodies and linkages. We briefly explore applications built on this formulation, including manipulation, latent interpolation, and sampling.

VectorAdam for Rotation Equivariant Geometry Optimization

The rise of geometric problems in machine learning has necessitated the development of equivariant methods, which preserve their output under the action of rotation or some other transformation. At the same time, the Adam optimization algorithm has proven remarkably effective across machine learning and even traditional tasks in geometric optimization. In this work, we observe that naively applying Adam to optimize vector-valued data is not rotation equivariant, due to per-coordinate moment updates, and in fact this leads to significant artifacts and biases in practice. We propose to resolve this deficiency with VectorAdam, a simple modification which makes Adam rotation-equivariant by accounting for the vector structure of optimization variables. We demonstrate this approach on problems in machine learning and traditional geometric optimization, showing that equivariant VectorAdam resolves the artifacts and biases of traditional Adam when applied to vector-valued data, with equivalent or even improved rates of convergence.