Approximately Piecewise E(3) Equivariant Point Networks
Paper and Code
Feb 13, 2024

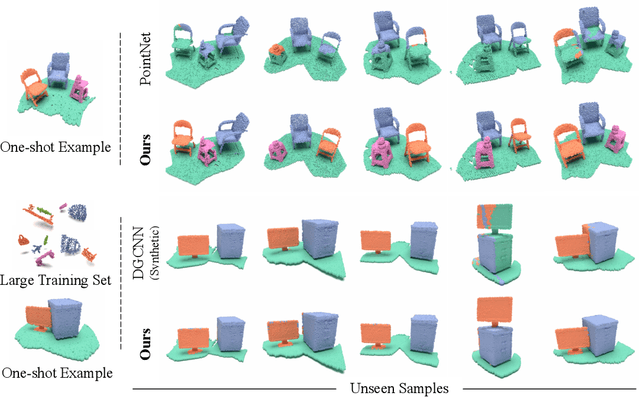
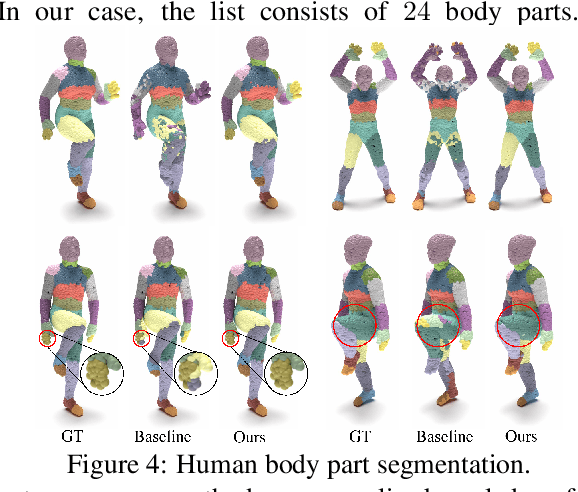
Integrating a notion of symmetry into point cloud neural networks is a provably effective way to improve their generalization capability. Of particular interest are $E(3)$ equivariant point cloud networks where Euclidean transformations applied to the inputs are preserved in the outputs. Recent efforts aim to extend networks that are $E(3)$ equivariant, to accommodate inputs made of multiple parts, each of which exhibits local $E(3)$ symmetry. In practical settings, however, the partitioning into individually transforming regions is unknown a priori. Errors in the partition prediction would unavoidably map to errors in respecting the true input symmetry. Past works have proposed different ways to predict the partition, which may exhibit uncontrolled errors in their ability to maintain equivariance to the actual partition. To this end, we introduce APEN: a general framework for constructing approximate piecewise-$E(3)$ equivariant point networks. Our primary insight is that functions that are equivariant with respect to a finer partition will also maintain equivariance in relation to the true partition. Leveraging this observation, we propose a design where the equivariance approximation error at each layers can be bounded solely in terms of (i) uncertainty quantification of the partition prediction, and (ii) bounds on the probability of failing to suggest a proper subpartition of the ground truth one. We demonstrate the effectiveness of APEN using two data types exemplifying part-based symmetry: (i) real-world scans of room scenes containing multiple furniture-type objects; and, (ii) human motions, characterized by articulated parts exhibiting rigid movement. Our empirical results demonstrate the advantage of integrating piecewise $E(3)$ symmetry into network design, showing a distinct improvement in generalization compared to prior works for both classification and segmentation tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge