Isometric Autoencoders

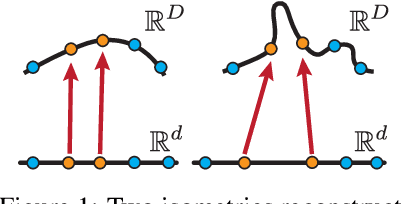
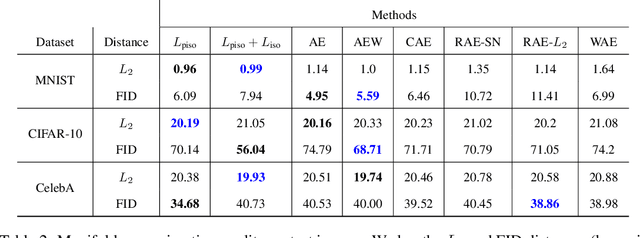
High dimensional data is often assumed to be concentrated near a low-dimensional manifold. Autoencoders (AE) is a popular technique to learn representations of such data by pushing it through a neural network with a low dimension bottleneck while minimizing a reconstruction error. Using high capacity AE often leads to a large collection of minimizers, many of which represent a low dimensional manifold that fits the data well but generalizes poorly. Two sources of bad generalization are: extrinsic, where the learned manifold possesses extraneous parts that are far from the data; and intrinsic, where the encoder and decoder introduce arbitrary distortion in the low dimensional parameterization. An approach taken to alleviate these issues is to add a regularizer that favors a particular solution; common regularizers promote sparsity, small derivatives, or robustness to noise. In this paper, we advocate an isometry (ie, distance preserving) regularizer. Specifically, our regularizer encourages: (i) the decoder to be an isometry; and (ii) the encoder to be a pseudo-isometry, where pseudo-isometry is an extension of an isometry with an orthogonal projection operator. In a nutshell, (i) preserves all geometric properties of the data such as volume, length, angle, and probability density. It fixes the intrinsic degree of freedom since any two isometric decoders to the same manifold will differ by a rigid motion. (ii) Addresses the extrinsic degree of freedom by minimizing derivatives in orthogonal directions to the manifold and hence disfavoring complicated manifold solutions. Experimenting with the isometry regularizer on dimensionality reduction tasks produces useful low-dimensional data representations, while incorporating it in AE models leads to an improved generalization.

Implicit Geometric Regularization for Learning Shapes

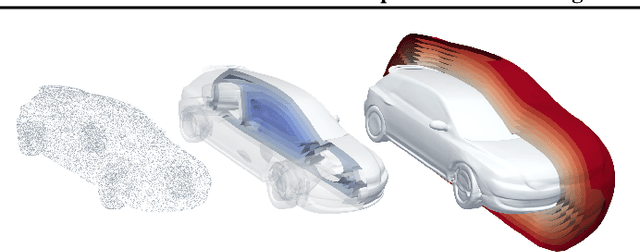
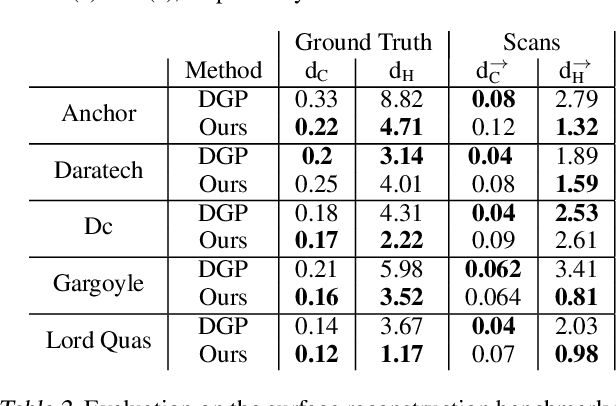
Representing shapes as level sets of neural networks has been recently proved to be useful for different shape analysis and reconstruction tasks So far, such representations were computed using either: (i) pre-computed implicit shape representations; or (ii) loss functions explicitly defined over the neural level sets. In this paper we offer a new paradigm for computing high fidelity implicit neural representations directly from raw data (i.e., point clouds, with or without normal information). We observe that a rather simple loss function, encouraging the neural network to vanish on the input point cloud and to have a unit norm gradient, possesses an implicit geometric regularization property that favors smooth and natural zero level set surfaces, avoiding bad zero-loss solutions. We provide a theoretical analysis of this property for the linear case, and show that, in practice, our method leads to state of the art implicit neural representations with higher level-of-details and fidelity compared to previous methods.