Hierarchical Autoregressive Transformers: Combining Byte-~and Word-Level Processing for Robust, Adaptable Language Models

Tokenization is a fundamental step in natural language processing, breaking text into units that computational models can process. While learned subword tokenizers have become the de-facto standard, they present challenges such as large vocabularies, limited adaptability to new domains or languages, and sensitivity to spelling errors and variations. To overcome these limitations, we investigate a hierarchical architecture for autoregressive language modelling that combines character-level and word-level processing. It employs a lightweight character-level encoder to convert character sequences into word embeddings, which are then processed by a word-level backbone model and decoded back into characters via a compact character-level decoder. This method retains the sequence compression benefits of word-level tokenization without relying on a rigid, predefined vocabulary. We demonstrate, at scales up to 7 billion parameters, that hierarchical transformers match the downstream task performance of subword-tokenizer-based models while exhibiting significantly greater robustness to input perturbations. Additionally, during continued pretraining on an out-of-domain language, our model trains almost twice as fast, achieves superior performance on the target language, and retains more of its previously learned knowledge. Hierarchical transformers pave the way for NLP systems that are more robust, flexible, and generalizable across languages and domains.

u-$μ$P: The Unit-Scaled Maximal Update Parametrization

The Maximal Update Parametrization ($\mu$P) aims to make the optimal hyperparameters (HPs) of a model independent of its size, allowing them to be swept using a cheap proxy model rather than the full-size target model. We present a new scheme, u-$\mu$P, which improves upon $\mu$P by combining it with Unit Scaling, a method for designing models that makes them easy to train in low-precision. The two techniques have a natural affinity: $\mu$P ensures that the scale of activations is independent of model size, and Unit Scaling ensures that activations, weights and gradients begin training with a scale of one. This synthesis opens the door to a simpler scheme, whose default values are near-optimal. This in turn facilitates a more efficient sweeping strategy, with u-$\mu$P models reaching a lower loss than comparable $\mu$P models and working out-of-the-box in FP8.

Choice of PEFT Technique in Continual Learning: Prompt Tuning is Not All You Need

Recent Continual Learning (CL) methods have combined pretrained Transformers with prompt tuning, a parameter-efficient fine-tuning (PEFT) technique. We argue that the choice of prompt tuning in prior works was an undefended and unablated decision, which has been uncritically adopted by subsequent research, but warrants further research to understand its implications. In this paper, we conduct this research and find that the choice of prompt tuning as a PEFT method hurts the overall performance of the CL system. To illustrate this, we replace prompt tuning with LoRA in two state-of-the-art continual learning methods: Learning to Prompt and S-Prompts. These variants consistently achieve higher accuracy across a wide range of domain-incremental and class-incremental benchmarks, while being competitive in inference speed. Our work highlights a crucial argument: unexamined choices can hinder progress in the field, and rigorous ablations, such as the PEFT method, are required to drive meaningful adoption of CL techniques in real-world applications.

A Negative Result on Gradient Matching for Selective Backprop

With increasing scale in model and dataset size, the training of deep neural networks becomes a massive computational burden. One approach to speed up the training process is Selective Backprop. For this approach, we perform a forward pass to obtain a loss value for each data point in a minibatch. The backward pass is then restricted to a subset of that minibatch, prioritizing high-loss examples. We build on this approach, but seek to improve the subset selection mechanism by choosing the (weighted) subset which best matches the mean gradient over the entire minibatch. We use the gradients w.r.t. the model's last layer as a cheap proxy, resulting in virtually no overhead in addition to the forward pass. At the same time, for our experiments we add a simple random selection baseline which has been absent from prior work. Surprisingly, we find that both the loss-based as well as the gradient-matching strategy fail to consistently outperform the random baseline.

Continual Learning with Low Rank Adaptation

Recent work using pretrained transformers has shown impressive performance when fine-tuned with data from the downstream problem of interest. However, they struggle to retain that performance when the data characteristics changes. In this paper, we focus on continual learning, where a pre-trained transformer is updated to perform well on new data, while retaining its performance on data it was previously trained on. Earlier works have tackled this primarily through methods inspired from prompt tuning. We question this choice, and investigate the applicability of Low Rank Adaptation (LoRA) to continual learning. On a range of domain-incremental learning benchmarks, our LoRA-based solution, CoLoR, yields state-of-the-art performance, while still being as parameter efficient as the prompt tuning based methods.

Renate: A Library for Real-World Continual Learning

Continual learning enables the incremental training of machine learning models on non-stationary data streams.While academic interest in the topic is high, there is little indication of the use of state-of-the-art continual learning algorithms in practical machine learning deployment. This paper presents Renate, a continual learning library designed to build real-world updating pipelines for PyTorch models. We discuss requirements for the use of continual learning algorithms in practice, from which we derive design principles for Renate. We give a high-level description of the library components and interfaces. Finally, we showcase the strengths of the library by presenting experimental results. Renate may be found at https://github.com/awslabs/renate.

PASHA: Efficient HPO with Progressive Resource Allocation

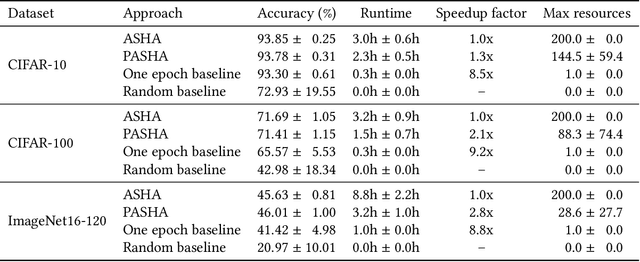
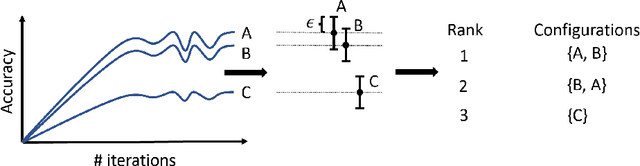
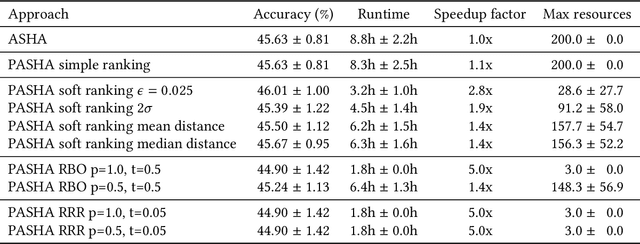
Hyperparameter optimization (HPO) and neural architecture search (NAS) are methods of choice to obtain the best-in-class machine learning models, but in practice they can be costly to run. When models are trained on large datasets, tuning them with HPO or NAS rapidly becomes prohibitively expensive for practitioners, even when efficient multi-fidelity methods are employed. We propose an approach to tackle the challenge of tuning machine learning models trained on large datasets with limited computational resources. Our approach, named PASHA, is able to dynamically allocate maximum resources for the tuning procedure depending on the need. The experimental comparison shows that PASHA identifies well-performing hyperparameter configurations and architectures while consuming significantly fewer computational resources than solutions like ASHA.

Gradient-Matching Coresets for Rehearsal-Based Continual Learning

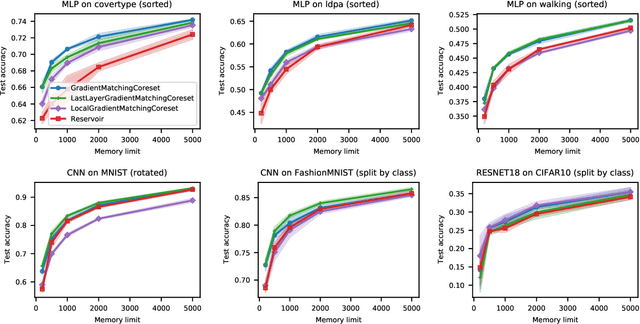
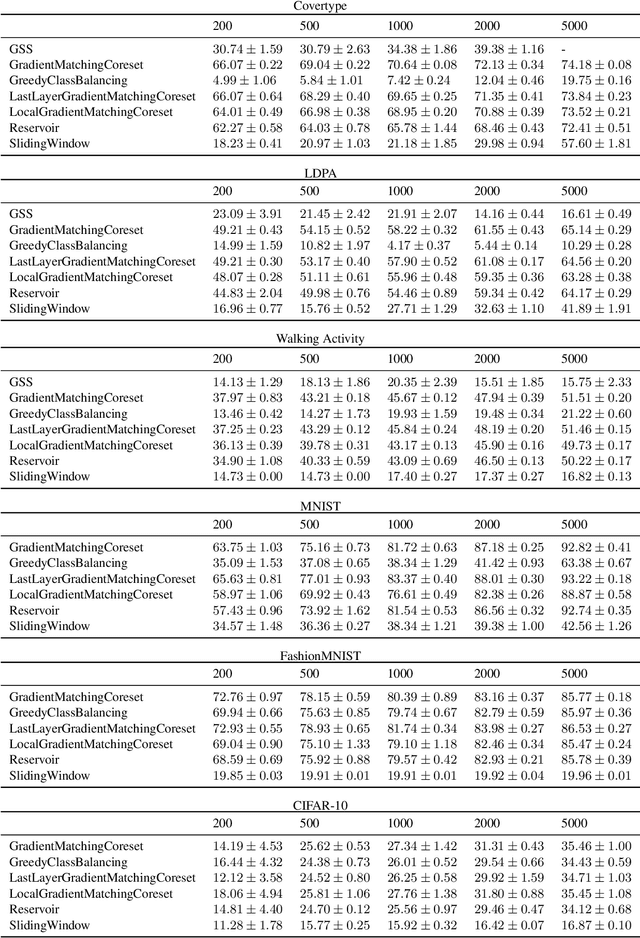
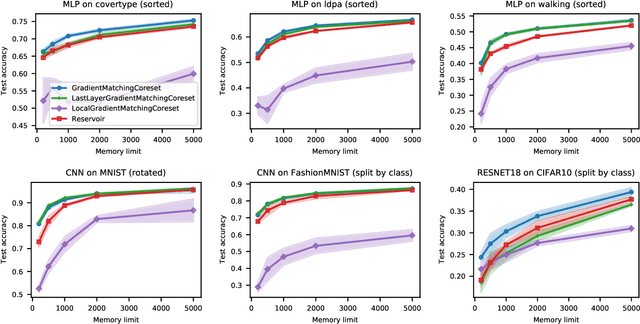
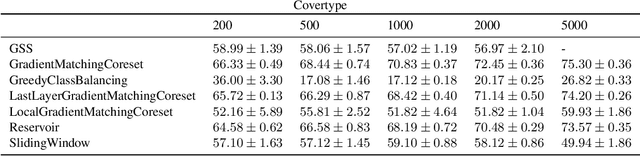
The goal of continual learning (CL) is to efficiently update a machine learning model with new data without forgetting previously-learned knowledge. Most widely-used CL methods rely on a rehearsal memory of data points to be reused while training on new data. Curating such a rehearsal memory to maintain a small, informative subset of all the data seen so far is crucial to the success of these methods. We devise a coreset selection method for rehearsal-based continual learning. Our method is based on the idea of gradient matching: The gradients induced by the coreset should match, as closely as possible, those induced by the original training dataset. Inspired by the neural tangent kernel theory, we perform this gradient matching across the model's initialization distribution, allowing us to extract a coreset without having to train the model first. We evaluate the method on a wide range of continual learning scenarios and demonstrate that it improves the performance of rehearsal-based CL methods compared to competing memory management strategies such as reservoir sampling.

Gradient-matching coresets for continual learning

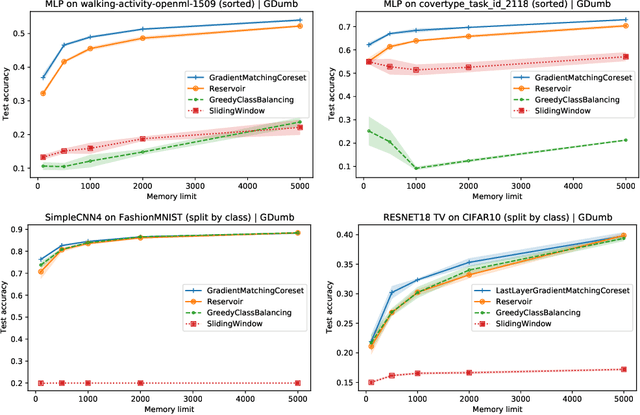
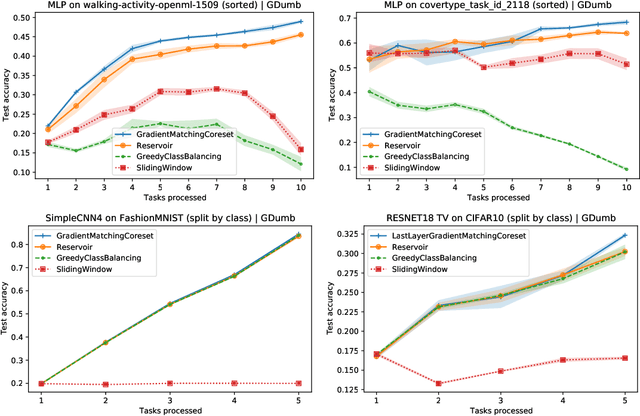
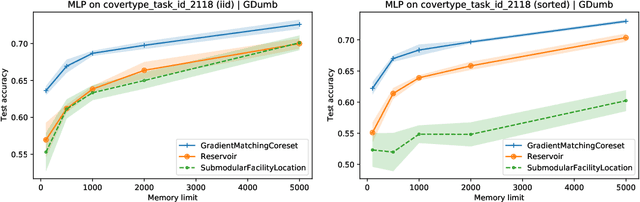
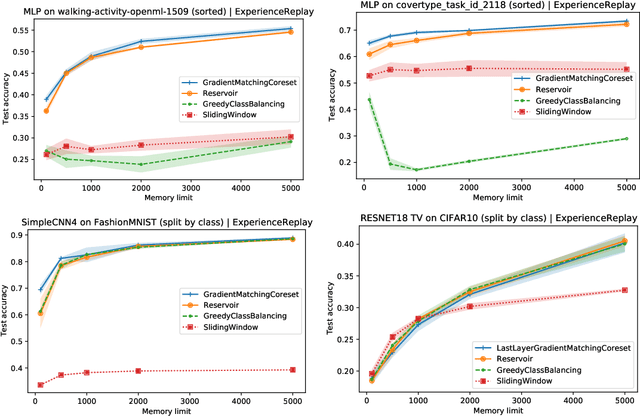
We devise a coreset selection method based on the idea of gradient matching: The gradients induced by the coreset should match, as closely as possible, those induced by the original training dataset. We evaluate the method in the context of continual learning, where it can be used to curate a rehearsal memory. Our method performs strong competitors such as reservoir sampling across a range of memory sizes.

Self-Tuning Stochastic Optimization with Curvature-Aware Gradient Filtering

Standard first-order stochastic optimization algorithms base their updates solely on the average mini-batch gradient, and it has been shown that tracking additional quantities such as the curvature can help de-sensitize common hyperparameters. Based on this intuition, we explore the use of exact per-sample Hessian-vector products and gradients to construct optimizers that are self-tuning and hyperparameter-free. Based on a dynamics model of the gradient, we derive a process which leads to a curvature-corrected, noise-adaptive online gradient estimate. The smoothness of our updates makes it more amenable to simple step size selection schemes, which we also base off of our estimates quantities. We prove that our model-based procedure converges in the noisy quadratic setting. Though we do not see similar gains in deep learning tasks, we can match the performance of well-tuned optimizers and ultimately, this is an interesting step for constructing self-tuning optimizers.