What does a deep neural network confidently perceive? The effective dimension of high certainty class manifolds and their low confidence boundaries

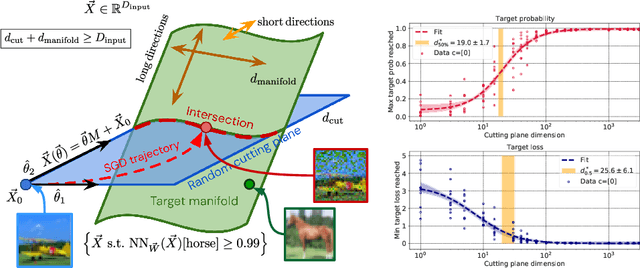
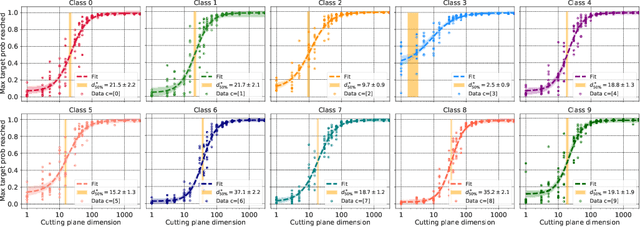
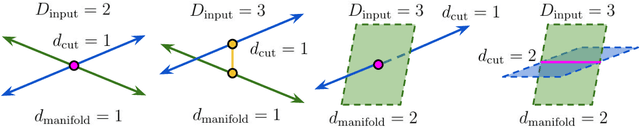
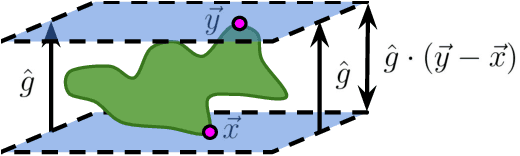
Deep neural network classifiers partition input space into high confidence regions for each class. The geometry of these class manifolds (CMs) is widely studied and intimately related to model performance; for example, the margin depends on CM boundaries. We exploit the notions of Gaussian width and Gordon's escape theorem to tractably estimate the effective dimension of CMs and their boundaries through tomographic intersections with random affine subspaces of varying dimension. We show several connections between the dimension of CMs, generalization, and robustness. In particular we investigate how CM dimension depends on 1) the dataset, 2) architecture (including ResNet, WideResNet \& Vision Transformer), 3) initialization, 4) stage of training, 5) class, 6) network width, 7) ensemble size, 8) label randomization, 9) training set size, and 10) robustness to data corruption. Together a picture emerges that higher performing and more robust models have higher dimensional CMs. Moreover, we offer a new perspective on ensembling via intersections of CMs. Our code is at https://github.com/stanislavfort/slice-dice-optimize/

Deep equilibrium networks are sensitive to initialization statistics

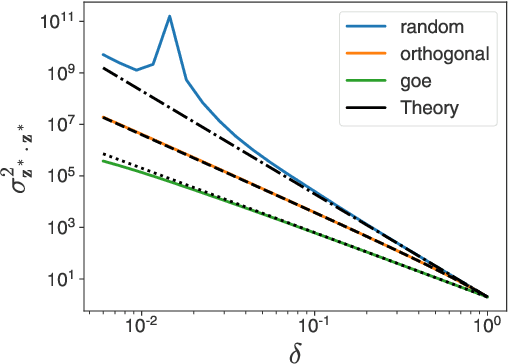
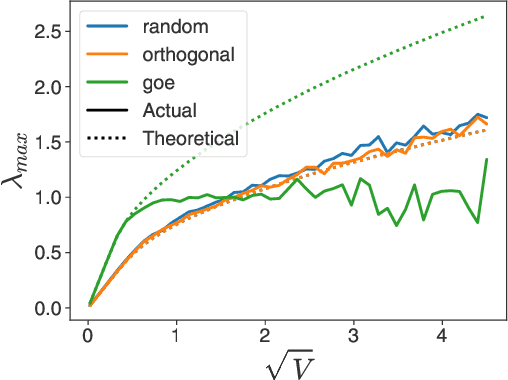
Deep equilibrium networks (DEQs) are a promising way to construct models which trade off memory for compute. However, theoretical understanding of these models is still lacking compared to traditional networks, in part because of the repeated application of a single set of weights. We show that DEQs are sensitive to the higher order statistics of the matrix families from which they are initialized. In particular, initializing with orthogonal or symmetric matrices allows for greater stability in training. This gives us a practical prescription for initializations which allow for training with a broader range of initial weight scales.

Fast Finite Width Neural Tangent Kernel

The Neural Tangent Kernel (NTK), defined as $\Theta_\theta^f(x_1, x_2) = \left[\partial f(\theta, x_1)\big/\partial \theta\right] \left[\partial f(\theta, x_2)\big/\partial \theta\right]^T$ where $\left[\partial f(\theta, \cdot)\big/\partial \theta\right]$ is a neural network (NN) Jacobian, has emerged as a central object of study in deep learning. In the infinite width limit, the NTK can sometimes be computed analytically and is useful for understanding training and generalization of NN architectures. At finite widths, the NTK is also used to better initialize NNs, compare the conditioning across models, perform architecture search, and do meta-learning. Unfortunately, the finite width NTK is notoriously expensive to compute, which severely limits its practical utility. We perform the first in-depth analysis of the compute and memory requirements for NTK computation in finite width networks. Leveraging the structure of neural networks, we further propose two novel algorithms that change the exponent of the compute and memory requirements of the finite width NTK, dramatically improving efficiency. Our algorithms can be applied in a black box fashion to any differentiable function, including those implementing neural networks. We open-source our implementations within the Neural Tangents package (arXiv:1912.02803) at https://github.com/google/neural-tangents.

Beyond the Imitation Game: Quantifying and extrapolating the capabilities of language models

Language models demonstrate both quantitative improvement and new qualitative capabilities with increasing scale. Despite their potentially transformative impact, these new capabilities are as yet poorly characterized. In order to inform future research, prepare for disruptive new model capabilities, and ameliorate socially harmful effects, it is vital that we understand the present and near-future capabilities and limitations of language models. To address this challenge, we introduce the Beyond the Imitation Game benchmark (BIG-bench). BIG-bench currently consists of 204 tasks, contributed by 442 authors across 132 institutions. Task topics are diverse, drawing problems from linguistics, childhood development, math, common-sense reasoning, biology, physics, social bias, software development, and beyond. BIG-bench focuses on tasks that are believed to be beyond the capabilities of current language models. We evaluate the behavior of OpenAI's GPT models, Google-internal dense transformer architectures, and Switch-style sparse transformers on BIG-bench, across model sizes spanning millions to hundreds of billions of parameters. In addition, a team of human expert raters performed all tasks in order to provide a strong baseline. Findings include: model performance and calibration both improve with scale, but are poor in absolute terms (and when compared with rater performance); performance is remarkably similar across model classes, though with benefits from sparsity; tasks that improve gradually and predictably commonly involve a large knowledge or memorization component, whereas tasks that exhibit "breakthrough" behavior at a critical scale often involve multiple steps or components, or brittle metrics; social bias typically increases with scale in settings with ambiguous context, but this can be improved with prompting.

Gradients are Not All You Need

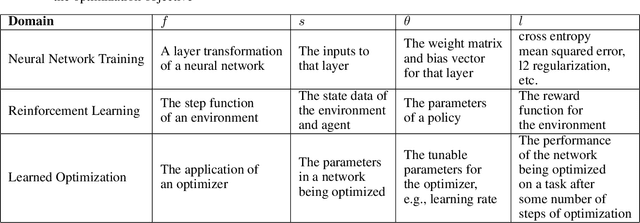
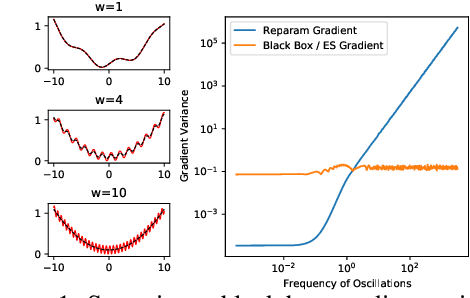
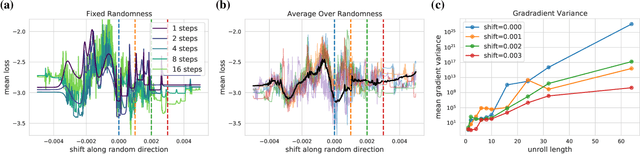
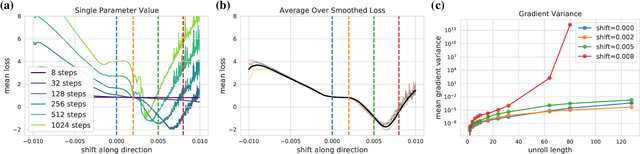
Differentiable programming techniques are widely used in the community and are responsible for the machine learning renaissance of the past several decades. While these methods are powerful, they have limits. In this short report, we discuss a common chaos based failure mode which appears in a variety of differentiable circumstances, ranging from recurrent neural networks and numerical physics simulation to training learned optimizers. We trace this failure to the spectrum of the Jacobian of the system under study, and provide criteria for when a practitioner might expect this failure to spoil their differentiation based optimization algorithms.

Rapid training of deep neural networks without skip connections or normalization layers using Deep Kernel Shaping

Using an extended and formalized version of the Q/C map analysis of Poole et al. (2016), along with Neural Tangent Kernel theory, we identify the main pathologies present in deep networks that prevent them from training fast and generalizing to unseen data, and show how these can be avoided by carefully controlling the "shape" of the network's initialization-time kernel function. We then develop a method called Deep Kernel Shaping (DKS), which accomplishes this using a combination of precise parameter initialization, activation function transformations, and small architectural tweaks, all of which preserve the model class. In our experiments we show that DKS enables SGD training of residual networks without normalization layers on Imagenet and CIFAR-10 classification tasks at speeds comparable to standard ResNetV2 and Wide-ResNet models, with only a small decrease in generalization performance. And when using K-FAC as the optimizer, we achieve similar results for networks without skip connections. Our results apply for a large variety of activation functions, including those which traditionally perform very badly, such as the logistic sigmoid. In addition to DKS, we contribute a detailed analysis of skip connections, normalization layers, special activation functions like RELU and SELU, and various initialization schemes, explaining their effectiveness as alternative (and ultimately incomplete) ways of "shaping" the network's initialization-time kernel.

Tilting the playing field: Dynamical loss functions for machine learning

We show that learning can be improved by using loss functions that evolve cyclically during training to emphasize one class at a time. In underparameterized networks, such dynamical loss functions can lead to successful training for networks that fail to find a deep minima of the standard cross-entropy loss. In overparameterized networks, dynamical loss functions can lead to better generalization. Improvement arises from the interplay of the changing loss landscape with the dynamics of the system as it evolves to minimize the loss. In particular, as the loss function oscillates, instabilities develop in the form of bifurcation cascades, which we study using the Hessian and Neural Tangent Kernel. Valleys in the landscape widen and deepen, and then narrow and rise as the loss landscape changes during a cycle. As the landscape narrows, the learning rate becomes too large and the network becomes unstable and bounces around the valley. This process ultimately pushes the system into deeper and wider regions of the loss landscape and is characterized by decreasing eigenvalues of the Hessian. This results in better regularized models with improved generalization performance.

Finite Versus Infinite Neural Networks: an Empirical Study

We perform a careful, thorough, and large scale empirical study of the correspondence between wide neural networks and kernel methods. By doing so, we resolve a variety of open questions related to the study of infinitely wide neural networks. Our experimental results include: kernel methods outperform fully-connected finite-width networks, but underperform convolutional finite width networks; neural network Gaussian process (NNGP) kernels frequently outperform neural tangent (NT) kernels; centered and ensembled finite networks have reduced posterior variance and behave more similarly to infinite networks; weight decay and the use of a large learning rate break the correspondence between finite and infinite networks; the NTK parameterization outperforms the standard parameterization for finite width networks; diagonal regularization of kernels acts similarly to early stopping; floating point precision limits kernel performance beyond a critical dataset size; regularized ZCA whitening improves accuracy; finite network performance depends non-monotonically on width in ways not captured by double descent phenomena; equivariance of CNNs is only beneficial for narrow networks far from the kernel regime. Our experiments additionally motivate an improved layer-wise scaling for weight decay which improves generalization in finite-width networks. Finally, we develop improved best practices for using NNGP and NT kernels for prediction, including a novel ensembling technique. Using these best practices we achieve state-of-the-art results on CIFAR-10 classification for kernels corresponding to each architecture class we consider.

Whitening and second order optimization both destroy information about the dataset, and can make generalization impossible

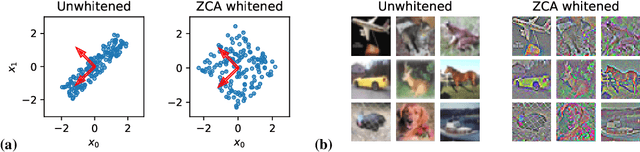
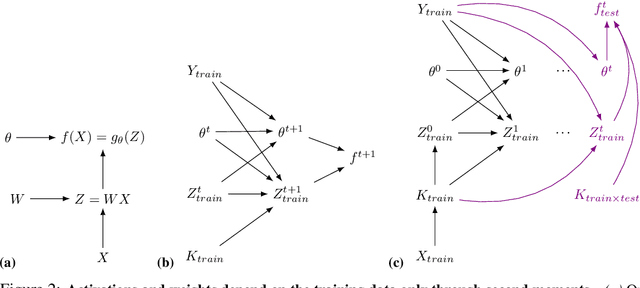
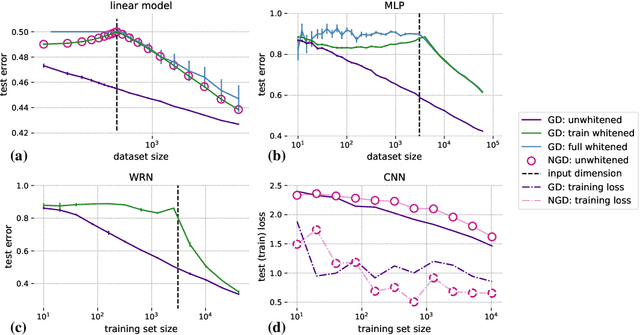
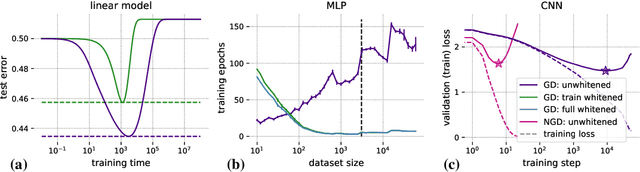
Machine learning is predicated on the concept of generalization: a model achieving low error on a sufficiently large training set should also perform well on novel samples from the same distribution. We show that both data whitening and second order optimization can harm or entirely prevent generalization. In general, model training harnesses information contained in the sample-sample second moment matrix of a dataset. For a general class of models, namely models with a fully connected first layer, we prove that the information contained in this matrix is the only information which can be used to generalize. Models trained using whitened data, or with certain second order optimization schemes, have less access to this information; in the high dimensional regime they have no access at all, producing models that generalize poorly or not at all. We experimentally verify these predictions for several architectures, and further demonstrate that generalization continues to be harmed even when theoretical requirements are relaxed. However, we also show experimentally that regularized second order optimization can provide a practical tradeoff, where training is still accelerated but less information is lost, and generalization can in some circumstances even improve.

On the infinite width limit of neural networks with a standard parameterization

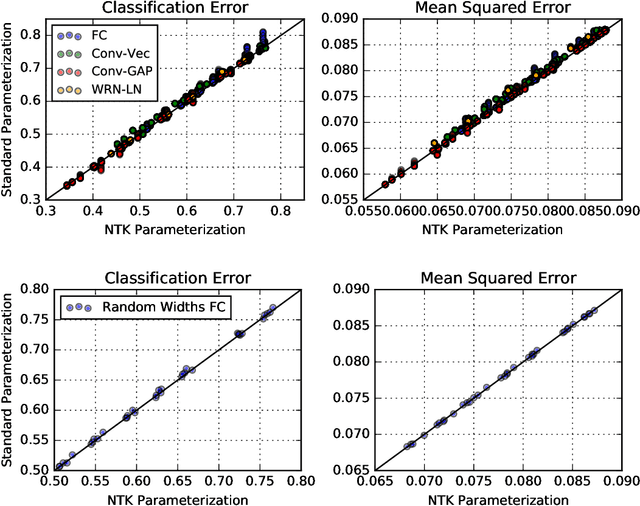
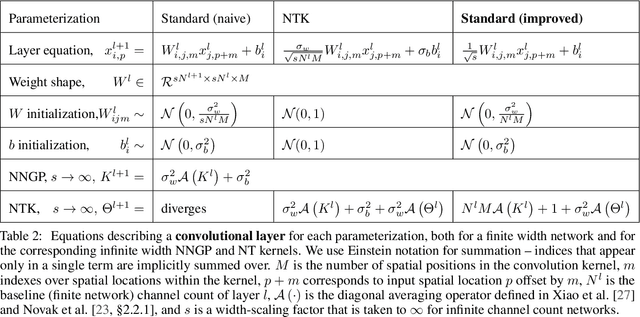
There are currently two parameterizations used to derive fixed kernels corresponding to infinite width neural networks, the NTK (Neural Tangent Kernel) parameterization and the naive standard parameterization. However, the extrapolation of both of these parameterizations to infinite width is problematic. The standard parameterization leads to a divergent neural tangent kernel while the NTK parameterization fails to capture crucial aspects of finite width networks such as: the dependence of training dynamics on relative layer widths, the relative training dynamics of weights and biases, and a nonstandard learning rate scale. Here we propose an improved extrapolation of the standard parameterization that preserves all of these properties as width is taken to infinity and yields a well-defined neural tangent kernel. We show experimentally that the resulting kernels typically achieve similar accuracy to those resulting from an NTK parameterization, but with better correspondence to the parameterization of typical finite width networks. Additionally, with careful tuning of width parameters, the improved standard parameterization kernels can outperform those stemming from an NTK parameterization. We release code implementing this improved standard parameterization as part of the Neural Tangents library at https://github.com/google/neural-tangents.