Dynamical loss functions shape landscape topography and improve learning in artificial neural networks

Dynamical loss functions are derived from standard loss functions used in supervised classification tasks, but they are modified such that the contribution from each class periodically increases and decreases. These oscillations globally alter the loss landscape without affecting the global minima. In this paper, we demonstrate how to transform cross-entropy and mean squared error into dynamical loss functions. We begin by discussing the impact of increasing the size of the neural network or the learning rate on the learning process. Building on this intuition, we propose several versions of dynamical loss functions and show how they significantly improve validation accuracy for networks of varying sizes. Finally, we explore how the landscape of these dynamical loss functions evolves during training, highlighting the emergence of instabilities that may be linked to edge-of-instability minimization.

Some thoughts on catastrophic forgetting and how to learn an algorithm

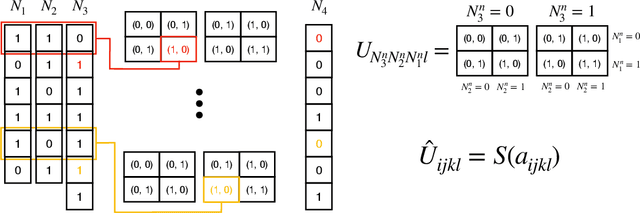
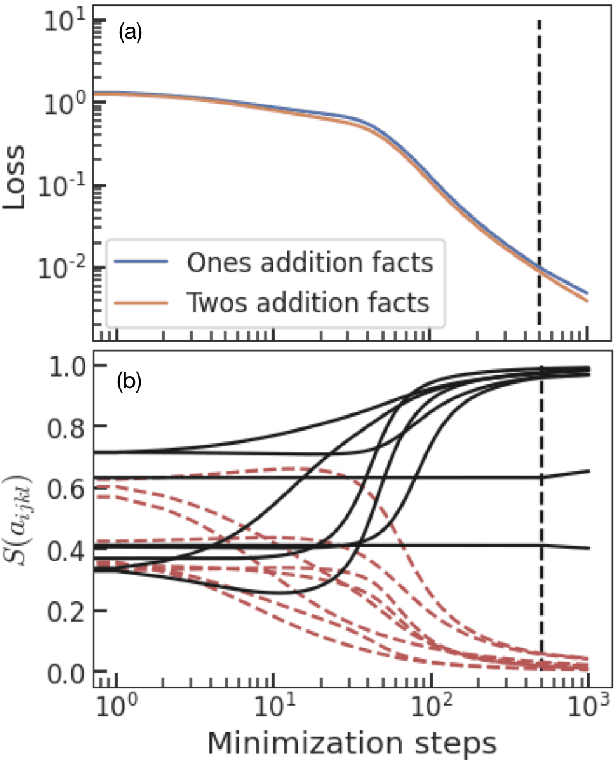
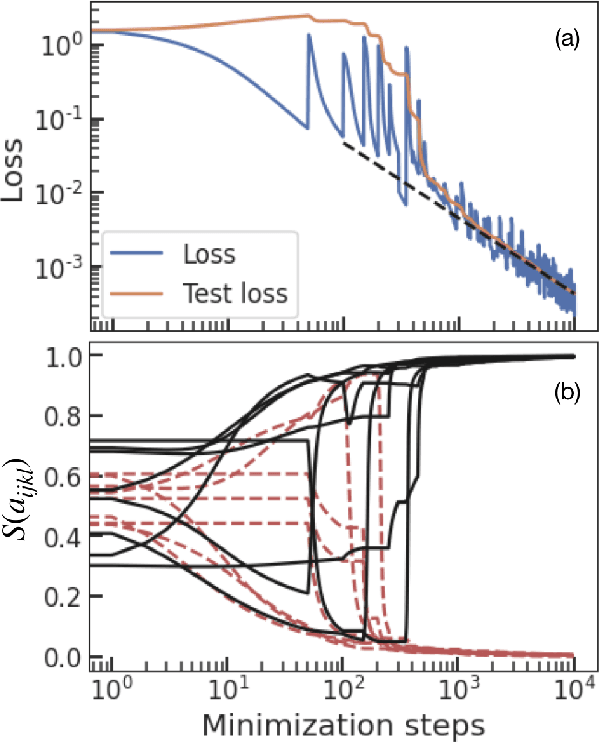
The work of McCloskey and Cohen popularized the concept of catastrophic interference. They used a neural network that tried to learn addition using two groups of examples as two different tasks. In their case, learning the second task rapidly deteriorated the acquired knowledge about the previous one. This could be a symptom of a fundamental problem: addition is an algorithmic task that should not be learned through pattern recognition. We propose to use a neural network with a different architecture that can be trained to recover the correct algorithm for the addition of binary numbers. We test it in the setting proposed by McCloskey and Cohen and training on random examples one by one. The neural network not only does not suffer from catastrophic forgetting but it improves its predictive power on unseen pairs of numbers as training progresses. This work emphasizes the importance that neural network architecture has for the emergence of catastrophic forgetting and introduces a neural network that is able to learn an algorithm.

Tilting the playing field: Dynamical loss functions for machine learning

We show that learning can be improved by using loss functions that evolve cyclically during training to emphasize one class at a time. In underparameterized networks, such dynamical loss functions can lead to successful training for networks that fail to find a deep minima of the standard cross-entropy loss. In overparameterized networks, dynamical loss functions can lead to better generalization. Improvement arises from the interplay of the changing loss landscape with the dynamics of the system as it evolves to minimize the loss. In particular, as the loss function oscillates, instabilities develop in the form of bifurcation cascades, which we study using the Hessian and Neural Tangent Kernel. Valleys in the landscape widen and deepen, and then narrow and rise as the loss landscape changes during a cycle. As the landscape narrows, the learning rate becomes too large and the network becomes unstable and bounces around the valley. This process ultimately pushes the system into deeper and wider regions of the loss landscape and is characterized by decreasing eigenvalues of the Hessian. This results in better regularized models with improved generalization performance.