A Gentle Introduction to Gradient-Based Optimization and Variational Inequalities for Machine Learning

The rapid progress in machine learning in recent years has been based on a highly productive connection to gradient-based optimization. Further progress hinges in part on a shift in focus from pattern recognition to decision-making and multi-agent problems. In these broader settings, new mathematical challenges emerge that involve equilibria and game theory instead of optima. Gradient-based methods remain essential -- given the high dimensionality and large scale of machine-learning problems -- but simple gradient descent is no longer the point of departure for algorithm design. We provide a gentle introduction to a broader framework for gradient-based algorithms in machine learning, beginning with saddle points and monotone games, and proceeding to general variational inequalities. While we provide convergence proofs for several of the algorithms that we present, our main focus is that of providing motivation and intuition.

Whitening and second order optimization both destroy information about the dataset, and can make generalization impossible

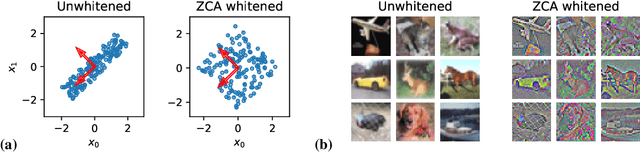
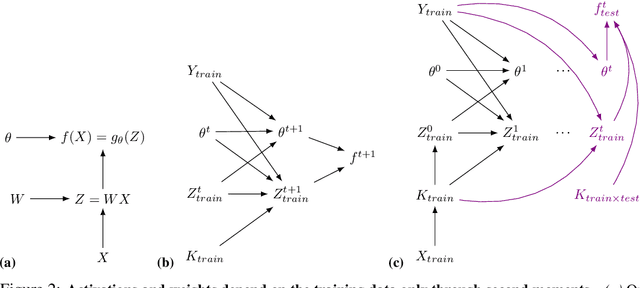
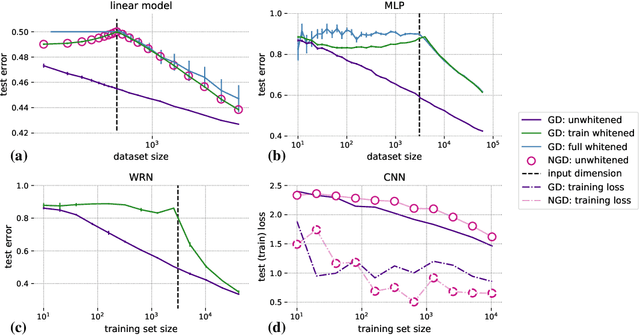
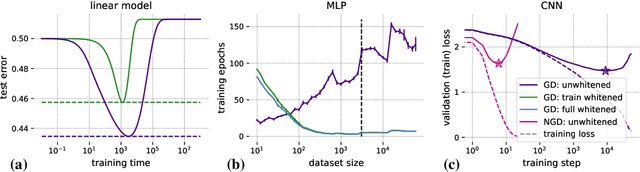
Machine learning is predicated on the concept of generalization: a model achieving low error on a sufficiently large training set should also perform well on novel samples from the same distribution. We show that both data whitening and second order optimization can harm or entirely prevent generalization. In general, model training harnesses information contained in the sample-sample second moment matrix of a dataset. For a general class of models, namely models with a fully connected first layer, we prove that the information contained in this matrix is the only information which can be used to generalize. Models trained using whitened data, or with certain second order optimization schemes, have less access to this information; in the high dimensional regime they have no access at all, producing models that generalize poorly or not at all. We experimentally verify these predictions for several architectures, and further demonstrate that generalization continues to be harmed even when theoretical requirements are relaxed. However, we also show experimentally that regularized second order optimization can provide a practical tradeoff, where training is still accelerated but less information is lost, and generalization can in some circumstances even improve.

Critical Point-Finding Methods Reveal Gradient-Flat Regions of Deep Network Losses

Despite the fact that the loss functions of deep neural networks are highly non-convex, gradient-based optimization algorithms converge to approximately the same performance from many random initial points. One thread of work has focused on explaining this phenomenon by characterizing the local curvature near critical points of the loss function, where the gradients are near zero, and demonstrating that neural network losses enjoy a no-bad-local-minima property and an abundance of saddle points. We report here that the methods used to find these putative critical points suffer from a bad local minima problem of their own: they often converge to or pass through regions where the gradient norm has a stationary point. We call these gradient-flat regions, since they arise when the gradient is approximately in the kernel of the Hessian, such that the loss is locally approximately linear, or flat, in the direction of the gradient. We describe how the presence of these regions necessitates care in both interpreting past results that claimed to find critical points of neural network losses and in designing second-order methods for optimizing neural networks.

Numerically Recovering the Critical Points of a Deep Linear Autoencoder

Numerically locating the critical points of non-convex surfaces is a long-standing problem central to many fields. Recently, the loss surfaces of deep neural networks have been explored to gain insight into outstanding questions in optimization, generalization, and network architecture design. However, the degree to which recently-proposed methods for numerically recovering critical points actually do so has not been thoroughly evaluated. In this paper, we examine this issue in a case for which the ground truth is known: the deep linear autoencoder. We investigate two sub-problems associated with numerical critical point identification: first, because of large parameter counts, it is infeasible to find all of the critical points for contemporary neural networks, necessitating sampling approaches whose characteristics are poorly understood; second, the numerical tolerance for accurately identifying a critical point is unknown, and conservative tolerances are difficult to satisfy. We first identify connections between recently-proposed methods and well-understood methods in other fields, including chemical physics, economics, and algebraic geometry. We find that several methods work well at recovering certain information about loss surfaces, but fail to take an unbiased sample of critical points. Furthermore, numerical tolerance must be very strict to ensure that numerically-identified critical points have similar properties to true analytical critical points. We also identify a recently-published Newton method for optimization that outperforms previous methods as a critical point-finding algorithm. We expect our results will guide future attempts to numerically study critical points in large nonlinear neural networks.