Whitening and second order optimization both destroy information about the dataset, and can make generalization impossible

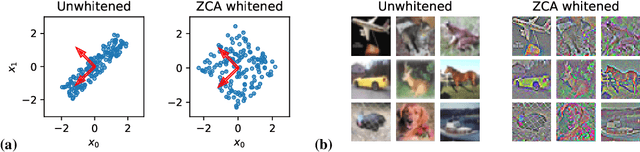
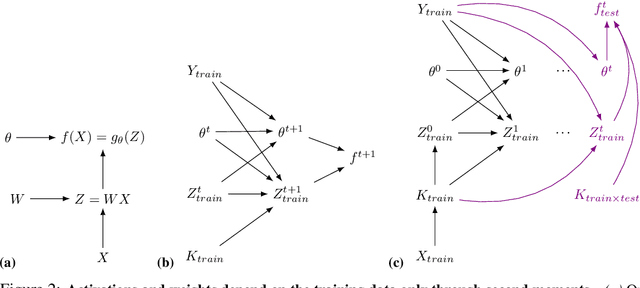
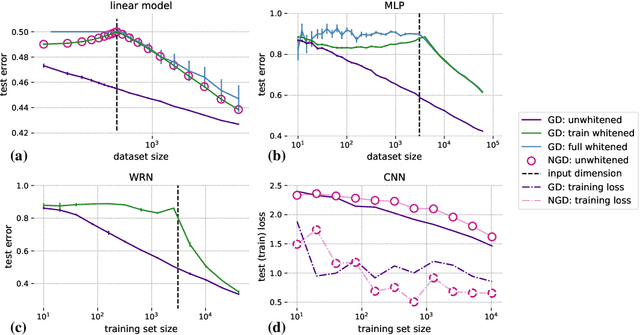
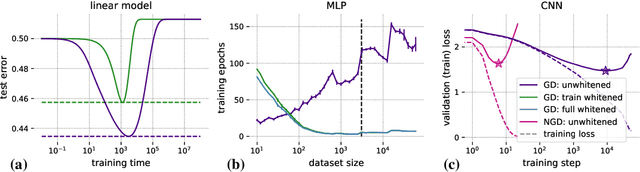
Machine learning is predicated on the concept of generalization: a model achieving low error on a sufficiently large training set should also perform well on novel samples from the same distribution. We show that both data whitening and second order optimization can harm or entirely prevent generalization. In general, model training harnesses information contained in the sample-sample second moment matrix of a dataset. For a general class of models, namely models with a fully connected first layer, we prove that the information contained in this matrix is the only information which can be used to generalize. Models trained using whitened data, or with certain second order optimization schemes, have less access to this information; in the high dimensional regime they have no access at all, producing models that generalize poorly or not at all. We experimentally verify these predictions for several architectures, and further demonstrate that generalization continues to be harmed even when theoretical requirements are relaxed. However, we also show experimentally that regularized second order optimization can provide a practical tradeoff, where training is still accelerated but less information is lost, and generalization can in some circumstances even improve.