What does a deep neural network confidently perceive? The effective dimension of high certainty class manifolds and their low confidence boundaries
Paper and Code
Oct 11, 2022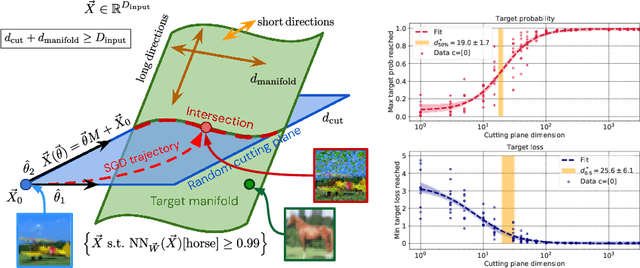
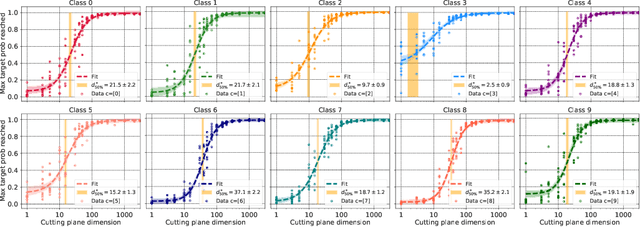
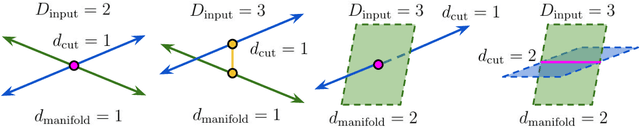
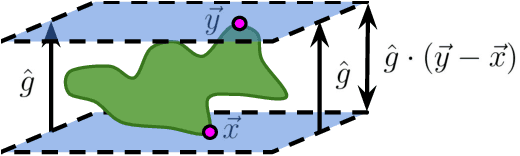
Deep neural network classifiers partition input space into high confidence regions for each class. The geometry of these class manifolds (CMs) is widely studied and intimately related to model performance; for example, the margin depends on CM boundaries. We exploit the notions of Gaussian width and Gordon's escape theorem to tractably estimate the effective dimension of CMs and their boundaries through tomographic intersections with random affine subspaces of varying dimension. We show several connections between the dimension of CMs, generalization, and robustness. In particular we investigate how CM dimension depends on 1) the dataset, 2) architecture (including ResNet, WideResNet \& Vision Transformer), 3) initialization, 4) stage of training, 5) class, 6) network width, 7) ensemble size, 8) label randomization, 9) training set size, and 10) robustness to data corruption. Together a picture emerges that higher performing and more robust models have higher dimensional CMs. Moreover, we offer a new perspective on ensembling via intersections of CMs. Our code is at https://github.com/stanislavfort/slice-dice-optimize/
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge