Ekin Dogus Cubuk
Shammie
System of Agentic AI for the Discovery of Metal-Organic Frameworks
Apr 18, 2025Abstract:Generative models and machine learning promise accelerated material discovery in MOFs for CO2 capture and water harvesting but face significant challenges navigating vast chemical spaces while ensuring synthetizability. Here, we present MOFGen, a system of Agentic AI comprising interconnected agents: a large language model that proposes novel MOF compositions, a diffusion model that generates crystal structures, quantum mechanical agents that optimize and filter candidates, and synthetic-feasibility agents guided by expert rules and machine learning. Trained on all experimentally reported MOFs and computational databases, MOFGen generated hundreds of thousands of novel MOF structures and synthesizable organic linkers. Our methodology was validated through high-throughput experiments and the successful synthesis of five "AI-dreamt" MOFs, representing a major step toward automated synthesizable material discovery.
A practical guide to machine learning interatomic potentials -- Status and future
Mar 12, 2025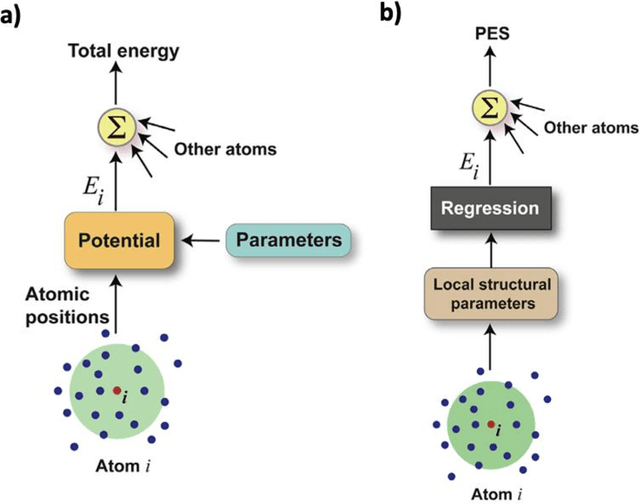

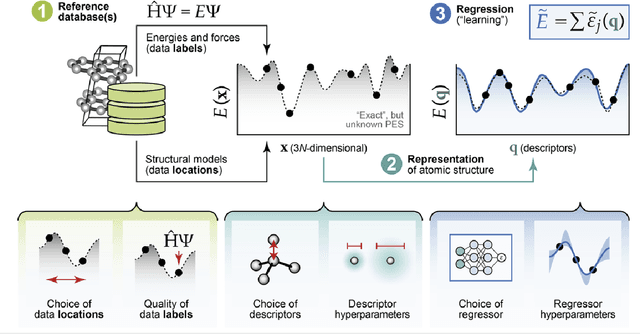
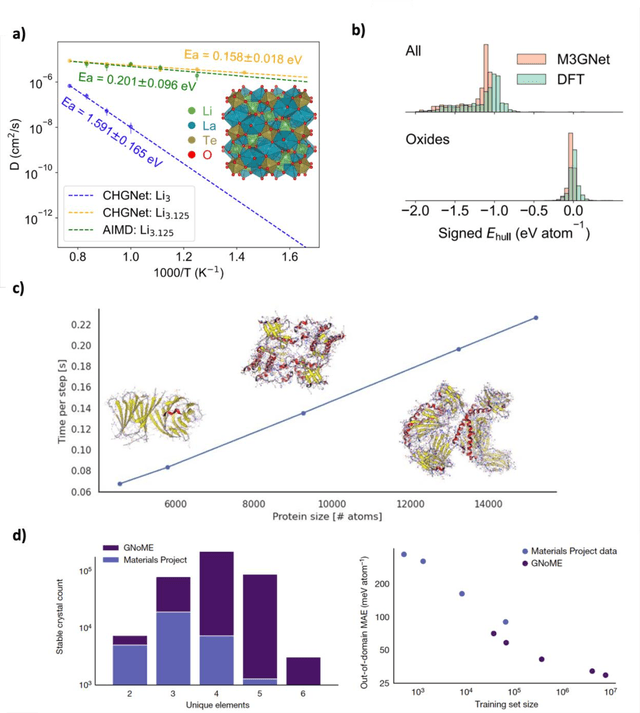
Abstract:The rapid development and large body of literature on machine learning interatomic potentials (MLIPs) can make it difficult to know how to proceed for researchers who are not experts but wish to use these tools. The spirit of this review is to help such researchers by serving as a practical, accessible guide to the state-of-the-art in MLIPs. This review paper covers a broad range of topics related to MLIPs, including (i) central aspects of how and why MLIPs are enablers of many exciting advancements in molecular modeling, (ii) the main underpinnings of different types of MLIPs, including their basic structure and formalism, (iii) the potentially transformative impact of universal MLIPs for both organic and inorganic systems, including an overview of the most recent advances, capabilities, downsides, and potential applications of this nascent class of MLIPs, (iv) a practical guide for estimating and understanding the execution speed of MLIPs, including guidance for users based on hardware availability, type of MLIP used, and prospective simulation size and time, (v) a manual for what MLIP a user should choose for a given application by considering hardware resources, speed requirements, energy and force accuracy requirements, as well as guidance for choosing pre-trained potentials or fitting a new potential from scratch, (vi) discussion around MLIP infrastructure, including sources of training data, pre-trained potentials, and hardware resources for training, (vii) summary of some key limitations of present MLIPs and current approaches to mitigate such limitations, including methods of including long-range interactions, handling magnetic systems, and treatment of excited states, and finally (viii) we finish with some more speculative thoughts on what the future holds for the development and application of MLIPs over the next 3-10+ years.
Scaling CLIP: A Comprehensive Analysis of Data, Architecture, and Training Strategies
Apr 12, 2024
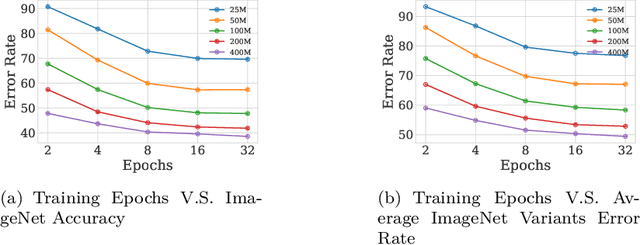
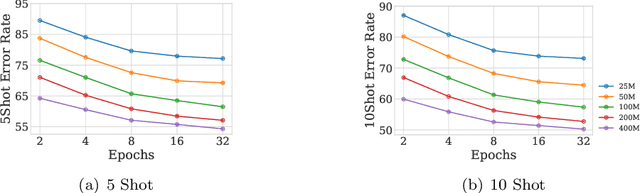
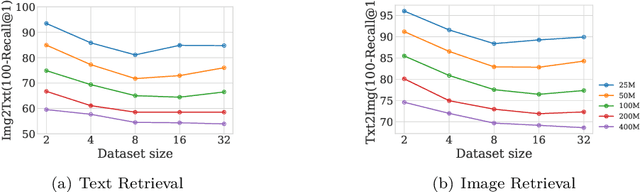
Abstract:This paper investigates the performance of the Contrastive Language-Image Pre-training (CLIP) when scaled down to limited computation budgets. We explore CLIP along three dimensions: data, architecture, and training strategies. With regards to data, we demonstrate the significance of high-quality training data and show that a smaller dataset of high-quality data can outperform a larger dataset with lower quality. We also examine how model performance varies with different dataset sizes, suggesting that smaller ViT models are better suited for smaller datasets, while larger models perform better on larger datasets with fixed compute. Additionally, we provide guidance on when to choose a CNN-based architecture or a ViT-based architecture for CLIP training. We compare four CLIP training strategies - SLIP, FLIP, CLIP, and CLIP+Data Augmentation - and show that the choice of training strategy depends on the available compute resource. Our analysis reveals that CLIP+Data Augmentation can achieve comparable performance to CLIP using only half of the training data. This work provides practical insights into how to effectively train and deploy CLIP models, making them more accessible and affordable for practical use in various applications.
AutoNumerics-Zero: Automated Discovery of State-of-the-Art Mathematical Functions
Dec 13, 2023Abstract:Computers calculate transcendental functions by approximating them through the composition of a few limited-precision instructions. For example, an exponential can be calculated with a Taylor series. These approximation methods were developed over the centuries by mathematicians, who emphasized the attainability of arbitrary precision. Computers, however, operate on few limited precision types, such as the popular float32. In this study, we show that when aiming for limited precision, existing approximation methods can be outperformed by programs automatically discovered from scratch by a simple evolutionary algorithm. In particular, over real numbers, our method can approximate the exponential function reaching orders of magnitude more precision for a given number of operations when compared to previous approaches. More practically, over float32 numbers and constrained to less than 1 ULP of error, the same method attains a speedup over baselines by generating code that triggers better XLA/LLVM compilation paths. In other words, in both cases, evolution searched a vast space of possible programs, without knowledge of mathematics, to discover previously unknown optimized approximations to high precision, for the first time. We also give evidence that these results extend beyond the exponential. The ubiquity of transcendental functions suggests that our method has the potential to reduce the cost of scientific computing applications.
Learning and Controlling Silicon Dopant Transitions in Graphene using Scanning Transmission Electron Microscopy
Nov 21, 2023Abstract:We introduce a machine learning approach to determine the transition dynamics of silicon atoms on a single layer of carbon atoms, when stimulated by the electron beam of a scanning transmission electron microscope (STEM). Our method is data-centric, leveraging data collected on a STEM. The data samples are processed and filtered to produce symbolic representations, which we use to train a neural network to predict transition probabilities. These learned transition dynamics are then leveraged to guide a single silicon atom throughout the lattice to pre-determined target destinations. We present empirical analyses that demonstrate the efficacy and generality of our approach.
Predicting emergence of crystals from amorphous matter with deep learning
Oct 02, 2023Abstract:Crystallization of the amorphous phases into metastable crystals plays a fundamental role in the formation of new matter, from geological to biological processes in nature to synthesis and development of new materials in the laboratory. Predicting the outcome of such phase transitions reliably would enable new research directions in these areas, but has remained beyond reach with molecular modeling or ab-initio methods. Here, we show that crystallization products of amorphous phases can be predicted in any inorganic chemistry by sampling the crystallization pathways of their local structural motifs at the atomistic level using universal deep learning potentials. We show that this approach identifies the crystal structures of polymorphs that initially nucleate from amorphous precursors with high accuracy across a diverse set of material systems, including polymorphic oxides, nitrides, carbides, fluorides, chlorides, chalcogenides, and metal alloys. Our results demonstrate that Ostwald's rule of stages can be exploited mechanistically at the molecular level to predictably access new metastable crystals from the amorphous phase in material synthesis.
Tied-Augment: Controlling Representation Similarity Improves Data Augmentation
May 22, 2023Abstract:Data augmentation methods have played an important role in the recent advance of deep learning models, and have become an indispensable component of state-of-the-art models in semi-supervised, self-supervised, and supervised training for vision. Despite incurring no additional latency at test time, data augmentation often requires more epochs of training to be effective. For example, even the simple flips-and-crops augmentation requires training for more than 5 epochs to improve performance, whereas RandAugment requires more than 90 epochs. We propose a general framework called Tied-Augment, which improves the efficacy of data augmentation in a wide range of applications by adding a simple term to the loss that can control the similarity of representations under distortions. Tied-Augment can improve state-of-the-art methods from data augmentation (e.g. RandAugment, mixup), optimization (e.g. SAM), and semi-supervised learning (e.g. FixMatch). For example, Tied-RandAugment can outperform RandAugment by 2.0% on ImageNet. Notably, using Tied-Augment, data augmentation can be made to improve generalization even when training for a few epochs and when fine-tuning. We open source our code at https://github.com/ekurtulus/tied-augment/tree/main.
LidarAugment: Searching for Scalable 3D LiDAR Data Augmentations
Oct 24, 2022



Abstract:Data augmentations are important in training high-performance 3D object detectors for point clouds. Despite recent efforts on designing new data augmentations, perhaps surprisingly, most state-of-the-art 3D detectors only use a few simple data augmentations. In particular, different from 2D image data augmentations, 3D data augmentations need to account for different representations of input data and require being customized for different models, which introduces significant overhead. In this paper, we resort to a search-based approach, and propose LidarAugment, a practical and effective data augmentation strategy for 3D object detection. Unlike previous approaches where all augmentation policies are tuned in an exponentially large search space, we propose to factorize and align the search space of each data augmentation, which cuts down the 20+ hyperparameters to 2, and significantly reduces the search complexity. We show LidarAugment can be customized for different model architectures with different input representations by a simple 2D grid search, and consistently improve both convolution-based UPillars/StarNet/RSN and transformer-based SWFormer. Furthermore, LidarAugment mitigates overfitting and allows us to scale up 3D detectors to much larger capacity. In particular, by combining with latest 3D detectors, our LidarAugment achieves a new state-of-the-art 74.8 mAPH L2 on Waymo Open Dataset.
What does a deep neural network confidently perceive? The effective dimension of high certainty class manifolds and their low confidence boundaries
Oct 11, 2022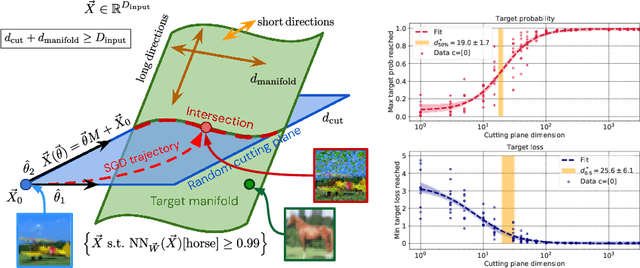
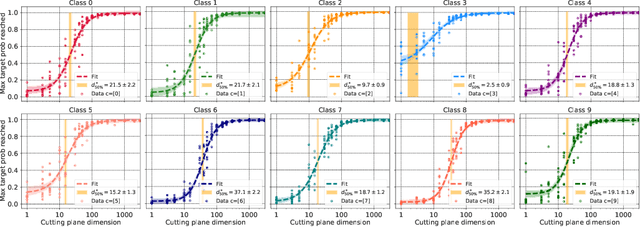
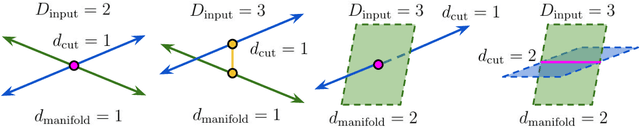
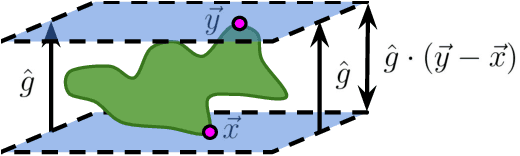
Abstract:Deep neural network classifiers partition input space into high confidence regions for each class. The geometry of these class manifolds (CMs) is widely studied and intimately related to model performance; for example, the margin depends on CM boundaries. We exploit the notions of Gaussian width and Gordon's escape theorem to tractably estimate the effective dimension of CMs and their boundaries through tomographic intersections with random affine subspaces of varying dimension. We show several connections between the dimension of CMs, generalization, and robustness. In particular we investigate how CM dimension depends on 1) the dataset, 2) architecture (including ResNet, WideResNet \& Vision Transformer), 3) initialization, 4) stage of training, 5) class, 6) network width, 7) ensemble size, 8) label randomization, 9) training set size, and 10) robustness to data corruption. Together a picture emerges that higher performing and more robust models have higher dimensional CMs. Moreover, we offer a new perspective on ensembling via intersections of CMs. Our code is at https://github.com/stanislavfort/slice-dice-optimize/
Beyond the Imitation Game: Quantifying and extrapolating the capabilities of language models
Jun 10, 2022Abstract:Language models demonstrate both quantitative improvement and new qualitative capabilities with increasing scale. Despite their potentially transformative impact, these new capabilities are as yet poorly characterized. In order to inform future research, prepare for disruptive new model capabilities, and ameliorate socially harmful effects, it is vital that we understand the present and near-future capabilities and limitations of language models. To address this challenge, we introduce the Beyond the Imitation Game benchmark (BIG-bench). BIG-bench currently consists of 204 tasks, contributed by 442 authors across 132 institutions. Task topics are diverse, drawing problems from linguistics, childhood development, math, common-sense reasoning, biology, physics, social bias, software development, and beyond. BIG-bench focuses on tasks that are believed to be beyond the capabilities of current language models. We evaluate the behavior of OpenAI's GPT models, Google-internal dense transformer architectures, and Switch-style sparse transformers on BIG-bench, across model sizes spanning millions to hundreds of billions of parameters. In addition, a team of human expert raters performed all tasks in order to provide a strong baseline. Findings include: model performance and calibration both improve with scale, but are poor in absolute terms (and when compared with rater performance); performance is remarkably similar across model classes, though with benefits from sparsity; tasks that improve gradually and predictably commonly involve a large knowledge or memorization component, whereas tasks that exhibit "breakthrough" behavior at a critical scale often involve multiple steps or components, or brittle metrics; social bias typically increases with scale in settings with ambiguous context, but this can be improved with prompting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge