Formal Conjectures: An Open and Evolving Benchmark for Verified Discovery in Mathematics

As automated reasoning systems advance rapidly, there is a growing need for research-level formal mathematical problems to accurately evaluate their capabilities. To address this, we present Formal Conjectures, an evolving benchmark of currently 2615 mathematical problem statements formalized in Lean 4. Sourced from areas of active mathematical research, the dataset features 1029 open research conjectures providing a zero-contamination benchmark for mathematical proof discovery, and 836 solved problems for proof autoformalization. Notably, the repository provides a structured interface connecting mathematicians who formalize and clarify problems with the AI systems and humans attempting to solve them. Demonstrating its immediate utility, the benchmark has already been leveraged to make new mathematical discoveries, including the resolution of open research conjectures. We describe our approach to ensuring the correctness of these formalizations in a collaborative open-source project where contributions stem from an active community. In this framework, AI-generated proofs and disproofs serve as a valuable auditing mechanism to iteratively improve the fidelity of the benchmark. Finally, we provide a standardized evaluation setup and report baseline results on frozen evaluation subsets, demonstrating a climbable signal that measures the current frontier of automated reasoning on research-level mathematics.

AutoNumerics-Zero: Automated Discovery of State-of-the-Art Mathematical Functions

Computers calculate transcendental functions by approximating them through the composition of a few limited-precision instructions. For example, an exponential can be calculated with a Taylor series. These approximation methods were developed over the centuries by mathematicians, who emphasized the attainability of arbitrary precision. Computers, however, operate on few limited precision types, such as the popular float32. In this study, we show that when aiming for limited precision, existing approximation methods can be outperformed by programs automatically discovered from scratch by a simple evolutionary algorithm. In particular, over real numbers, our method can approximate the exponential function reaching orders of magnitude more precision for a given number of operations when compared to previous approaches. More practically, over float32 numbers and constrained to less than 1 ULP of error, the same method attains a speedup over baselines by generating code that triggers better XLA/LLVM compilation paths. In other words, in both cases, evolution searched a vast space of possible programs, without knowledge of mathematics, to discover previously unknown optimized approximations to high precision, for the first time. We also give evidence that these results extend beyond the exponential. The ubiquity of transcendental functions suggests that our method has the potential to reduce the cost of scientific computing applications.

Intelligent Matrix Exponentiation

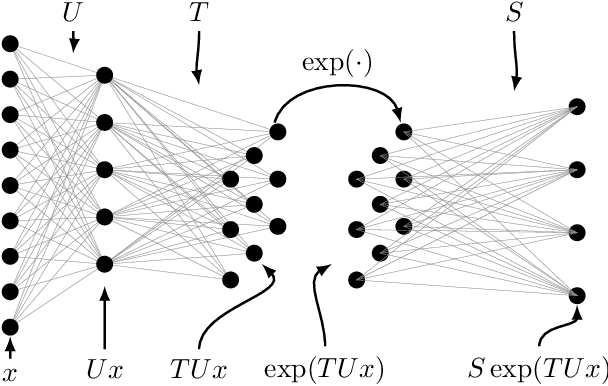
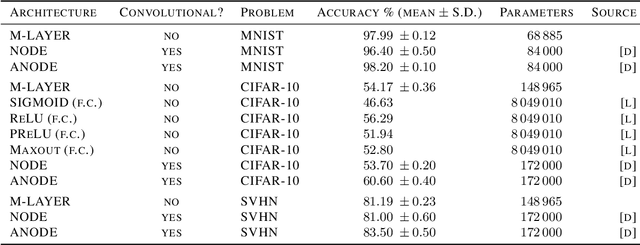
We present a novel machine learning architecture that uses the exponential of a single input-dependent matrix as its only nonlinearity. The mathematical simplicity of this architecture allows a detailed analysis of its behaviour, providing robustness guarantees via Lipschitz bounds. Despite its simplicity, a single matrix exponential layer already provides universal approximation properties and can learn fundamental functions of the input, such as periodic functions or multivariate polynomials. This architecture outperforms other general-purpose architectures on benchmark problems, including CIFAR-10, using substantially fewer parameters.