On backpropagating Hessians through ODEs

We discuss the problem of numerically backpropagating Hessians through ordinary differential equations (ODEs) in various contexts and elucidate how different approaches may be favourable in specific situations. We discuss both theoretical and pragmatic aspects such as, respectively, bounds on computational effort and typical impact of framework overhead. Focusing on the approach of hand-implemented ODE-backpropagation, we develop the computation for the Hessian of orbit-nonclosure for a mechanical system. We also clarify the mathematical framework for extending the backward-ODE-evolution of the costate-equation to Hessians, in its most generic form. Some calculations, such as that of the Hessian for orbit non-closure, are performed in a language, defined in terms of a formal grammar, that we introduce to facilitate the tracking of intermediate quantities. As pedagogical examples, we discuss the Hessian of orbit-nonclosure for the higher dimensional harmonic oscillator and conceptually related problems in Newtonian gravitational theory. In particular, applying our approach to the figure-8 three-body orbit, we readily rediscover a distorted-figure-8 solution originally described by Sim\'o. Possible applications may include: improvements to training of `neural ODE'- type deep learning with second-order methods, numerical analysis of quantum corrections around classical paths, and, more broadly, studying options for adjusting an ODE's initial configuration such that the impact on some given objective function is small.

Single-Photon Image Classification

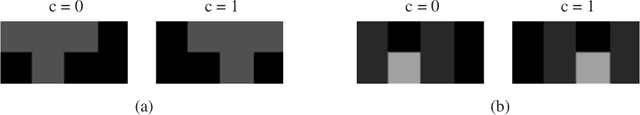
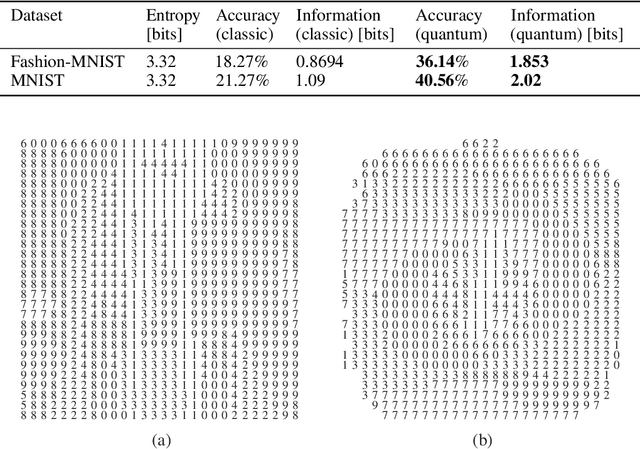
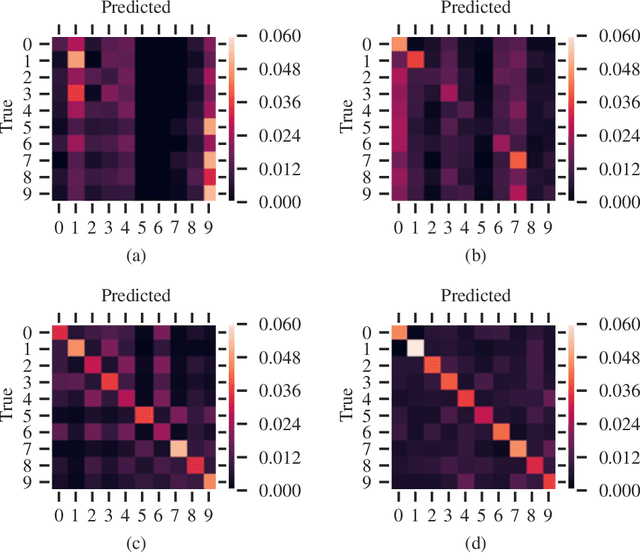
Quantum computing-based machine learning mainly focuses on quantum computing hardware that is experimentally challenging to realize due to requiring quantum gates that operate at very low temperature. Instead, we demonstrate the existence of a lower performance and much lower effort island on the accuracy-vs-qubits graph that may well be experimentally accessible with room temperature optics. This high temperature "quantum computing toy model" is nevertheless interesting to study as it allows rather accessible explanations of key concepts in quantum computing, in particular interference, entanglement, and the measurement process. We specifically study the problem of classifying an example from the MNIST and Fashion-MNIST datasets, subject to the constraint that we have to make a prediction after the detection of the very first photon that passed a coherently illuminated filter showing the example. Whereas a classical set-up in which a photon is detected after falling on one of the~$28\times 28$ image pixels is limited to a (maximum likelihood estimation) accuracy of~$21.27\%$ for MNIST, respectively $18.27\%$ for Fashion-MNIST, we show that the theoretically achievable accuracy when exploiting inference by optically transforming the quantum state of the photon is at least $41.27\%$ for MNIST, respectively $36.14\%$ for Fashion-MNIST. We show in detail how to train the corresponding transformation with TensorFlow and also explain how this example can serve as a teaching tool for the measurement process in quantum mechanics.

Intelligent Matrix Exponentiation

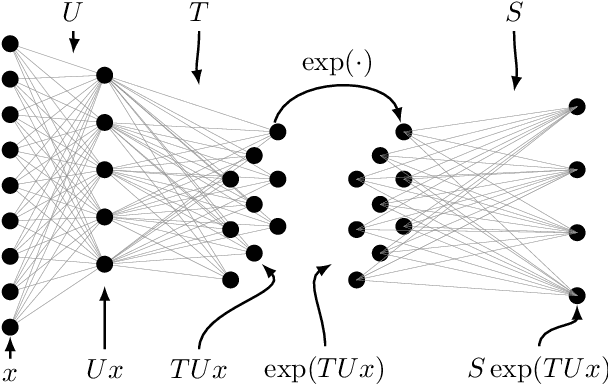
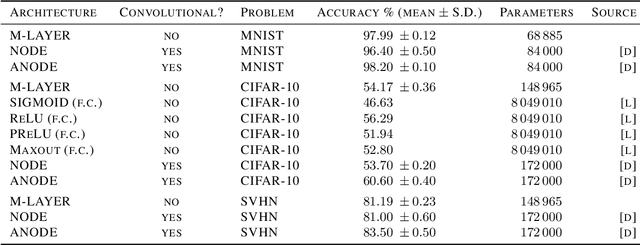
We present a novel machine learning architecture that uses the exponential of a single input-dependent matrix as its only nonlinearity. The mathematical simplicity of this architecture allows a detailed analysis of its behaviour, providing robustness guarantees via Lipschitz bounds. Despite its simplicity, a single matrix exponential layer already provides universal approximation properties and can learn fundamental functions of the input, such as periodic functions or multivariate polynomials. This architecture outperforms other general-purpose architectures on benchmark problems, including CIFAR-10, using substantially fewer parameters.

Temporal coding in spiking neural networks with alpha synaptic function

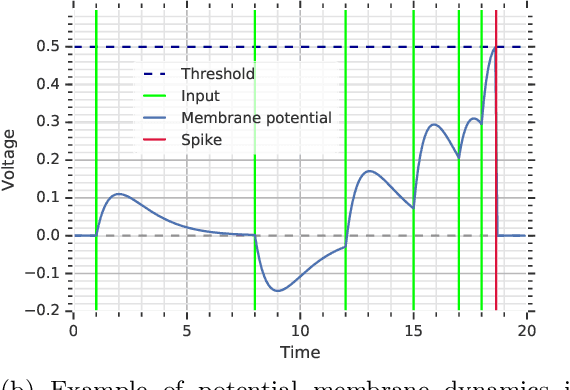
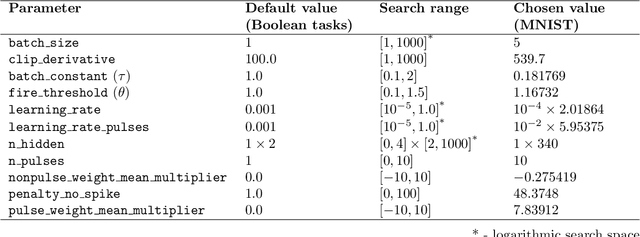
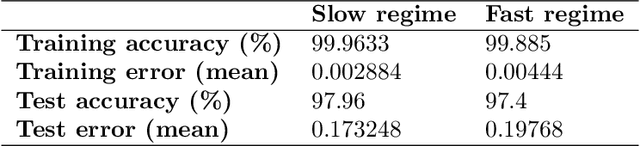
The timing of individual neuronal spikes is essential for biological brains to make fast responses to sensory stimuli. However, conventional artificial neural networks lack the intrinsic temporal coding ability present in biological networks. We propose a spiking neural network model that encodes information in the relative timing of individual neuron spikes. In classification tasks, the output of the network is indicated by the first neuron to spike in the output layer. This temporal coding scheme allows the supervised training of the network with backpropagation, using locally exact derivatives of the postsynaptic spike times with respect to presynaptic spike times. The network operates using a biologically-plausible alpha synaptic transfer function. Additionally, we use trainable synchronisation pulses that provide bias, add flexibility during training and exploit the decay part of the alpha function. We show that such networks can be trained successfully on noisy Boolean logic tasks and on the MNIST dataset encoded in time. The results show that the spiking neural network outperforms comparable spiking models on MNIST and achieves similar quality to fully connected conventional networks with the same architecture. We also find that the spiking network spontaneously discovers two operating regimes, mirroring the accuracy-speed trade-off observed in human decision-making: a slow regime, where a decision is taken after all hidden neurons have spiked and the accuracy is very high, and a fast regime, where a decision is taken very fast but the accuracy is lower. These results demonstrate the computational power of spiking networks with biological characteristics that encode information in the timing of individual neurons. By studying temporal coding in spiking networks, we aim to create building blocks towards energy-efficient and more complex biologically-inspired neural architectures.