Does It Make Sense to Speak of Introspection in Large Language Models?

Large language models (LLMs) exhibit compelling linguistic behaviour, and sometimes offer self-reports, that is to say statements about their own nature, inner workings, or behaviour. In humans, such reports are often attributed to a faculty of introspection and are typically linked to consciousness. This raises the question of how to interpret self-reports produced by LLMs, given their increasing linguistic fluency and cognitive capabilities. To what extent (if any) can the concept of introspection be meaningfully applied to LLMs? Here, we present and critique two examples of apparent introspective self-report from LLMs. In the first example, an LLM attempts to describe the process behind its own "creative" writing, and we argue this is not a valid example of introspection. In the second example, an LLM correctly infers the value of its own temperature parameter, and we argue that this can be legitimately considered a minimal example of introspection, albeit one that is (presumably) not accompanied by conscious experience.

Decoupling the components of geometric understanding in Vision Language Models

Understanding geometry relies heavily on vision. In this work, we evaluate whether state-of-the-art vision language models (VLMs) can understand simple geometric concepts. We use a paradigm from cognitive science that isolates visual understanding of simple geometry from the many other capabilities it is often conflated with such as reasoning and world knowledge. We compare model performance with human adults from the USA, as well as with prior research on human adults without formal education from an Amazonian indigenous group. We find that VLMs consistently underperform both groups of human adults, although they succeed with some concepts more than others. We also find that VLM geometric understanding is more brittle than human understanding, and is not robust when tasks require mental rotation. This work highlights interesting differences in the origin of geometric understanding in humans and machines -- e.g. from printed materials used in formal education vs. interactions with the physical world or a combination of the two -- and a small step toward understanding these differences.

Can LLMs make trade-offs involving stipulated pain and pleasure states?

Pleasure and pain play an important role in human decision making by providing a common currency for resolving motivational conflicts. While Large Language Models (LLMs) can generate detailed descriptions of pleasure and pain experiences, it is an open question whether LLMs can recreate the motivational force of pleasure and pain in choice scenarios - a question which may bear on debates about LLM sentience, understood as the capacity for valenced experiential states. We probed this question using a simple game in which the stated goal is to maximise points, but where either the points-maximising option is said to incur a pain penalty or a non-points-maximising option is said to incur a pleasure reward, providing incentives to deviate from points-maximising behaviour. Varying the intensity of the pain penalties and pleasure rewards, we found that Claude 3.5 Sonnet, Command R+, GPT-4o, and GPT-4o mini each demonstrated at least one trade-off in which the majority of responses switched from points-maximisation to pain-minimisation or pleasure-maximisation after a critical threshold of stipulated pain or pleasure intensity is reached. LLaMa 3.1-405b demonstrated some graded sensitivity to stipulated pleasure rewards and pain penalties. Gemini 1.5 Pro and PaLM 2 prioritised pain-avoidance over points-maximisation regardless of intensity, while tending to prioritise points over pleasure regardless of intensity. We discuss the implications of these findings for debates about the possibility of LLM sentience.

Intelligent Matrix Exponentiation

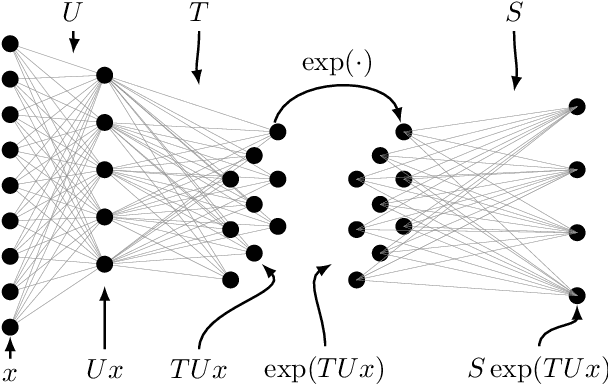
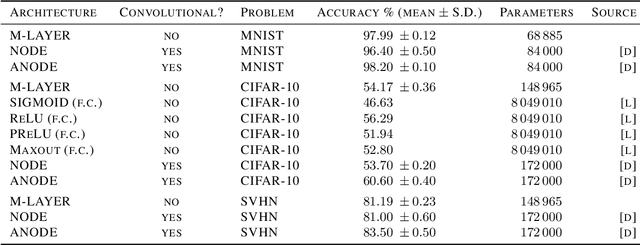
We present a novel machine learning architecture that uses the exponential of a single input-dependent matrix as its only nonlinearity. The mathematical simplicity of this architecture allows a detailed analysis of its behaviour, providing robustness guarantees via Lipschitz bounds. Despite its simplicity, a single matrix exponential layer already provides universal approximation properties and can learn fundamental functions of the input, such as periodic functions or multivariate polynomials. This architecture outperforms other general-purpose architectures on benchmark problems, including CIFAR-10, using substantially fewer parameters.

Temporal coding in spiking neural networks with alpha synaptic function

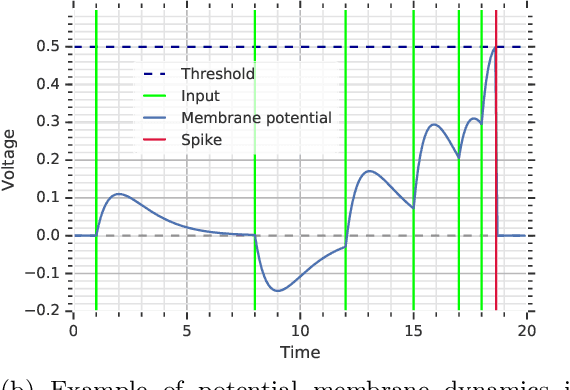
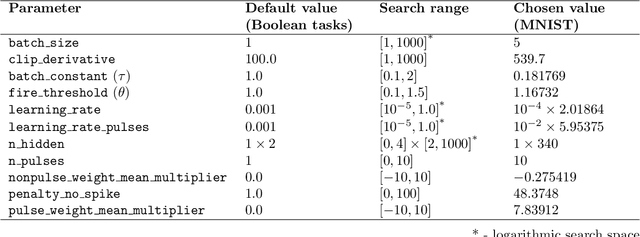
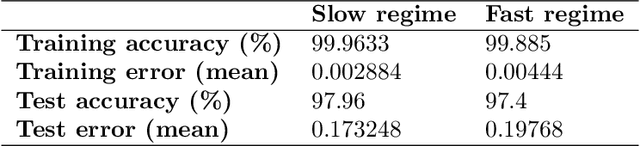
The timing of individual neuronal spikes is essential for biological brains to make fast responses to sensory stimuli. However, conventional artificial neural networks lack the intrinsic temporal coding ability present in biological networks. We propose a spiking neural network model that encodes information in the relative timing of individual neuron spikes. In classification tasks, the output of the network is indicated by the first neuron to spike in the output layer. This temporal coding scheme allows the supervised training of the network with backpropagation, using locally exact derivatives of the postsynaptic spike times with respect to presynaptic spike times. The network operates using a biologically-plausible alpha synaptic transfer function. Additionally, we use trainable synchronisation pulses that provide bias, add flexibility during training and exploit the decay part of the alpha function. We show that such networks can be trained successfully on noisy Boolean logic tasks and on the MNIST dataset encoded in time. The results show that the spiking neural network outperforms comparable spiking models on MNIST and achieves similar quality to fully connected conventional networks with the same architecture. We also find that the spiking network spontaneously discovers two operating regimes, mirroring the accuracy-speed trade-off observed in human decision-making: a slow regime, where a decision is taken after all hidden neurons have spiked and the accuracy is very high, and a fast regime, where a decision is taken very fast but the accuracy is lower. These results demonstrate the computational power of spiking networks with biological characteristics that encode information in the timing of individual neurons. By studying temporal coding in spiking networks, we aim to create building blocks towards energy-efficient and more complex biologically-inspired neural architectures.