Deep equilibrium networks are sensitive to initialization statistics
Paper and Code
Jul 19, 2022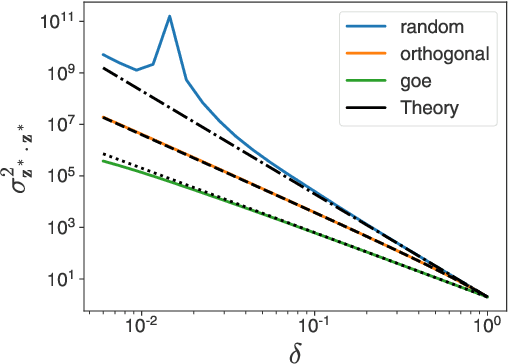


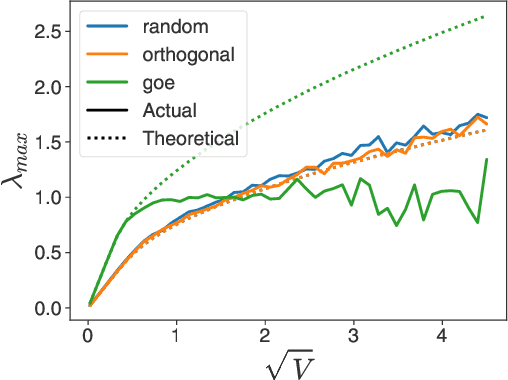
Deep equilibrium networks (DEQs) are a promising way to construct models which trade off memory for compute. However, theoretical understanding of these models is still lacking compared to traditional networks, in part because of the repeated application of a single set of weights. We show that DEQs are sensitive to the higher order statistics of the matrix families from which they are initialized. In particular, initializing with orthogonal or symmetric matrices allows for greater stability in training. This gives us a practical prescription for initializations which allow for training with a broader range of initial weight scales.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge