On a continuous time model of gradient descent dynamics and instability in deep learning

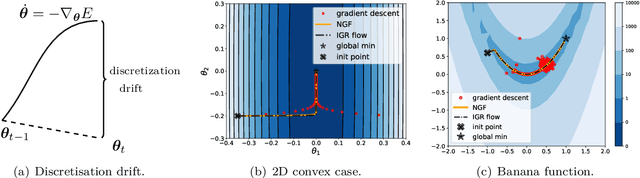
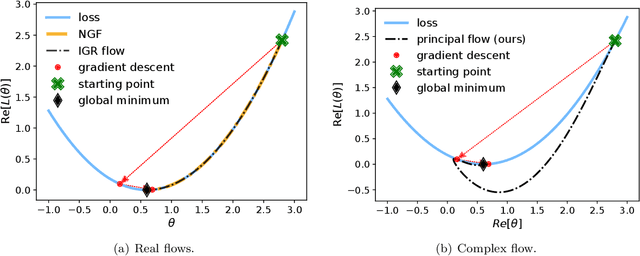
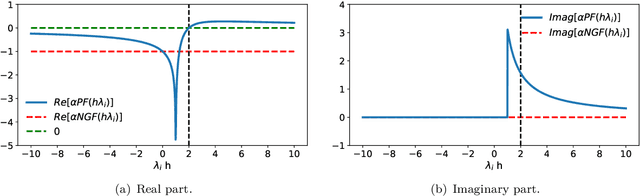
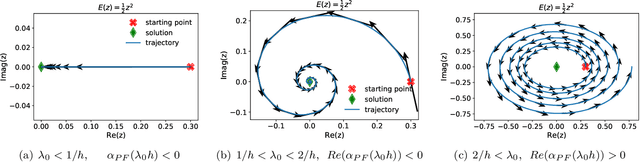
The recipe behind the success of deep learning has been the combination of neural networks and gradient-based optimization. Understanding the behavior of gradient descent however, and particularly its instability, has lagged behind its empirical success. To add to the theoretical tools available to study gradient descent we propose the principal flow (PF), a continuous time flow that approximates gradient descent dynamics. To our knowledge, the PF is the only continuous flow that captures the divergent and oscillatory behaviors of gradient descent, including escaping local minima and saddle points. Through its dependence on the eigendecomposition of the Hessian the PF sheds light on the recently observed edge of stability phenomena in deep learning. Using our new understanding of instability we propose a learning rate adaptation method which enables us to control the trade-off between training stability and test set evaluation performance.

Training Generative Adversarial Networks by Solving Ordinary Differential Equations

The instability of Generative Adversarial Network (GAN) training has frequently been attributed to gradient descent. Consequently, recent methods have aimed to tailor the models and training procedures to stabilise the discrete updates. In contrast, we study the continuous-time dynamics induced by GAN training. Both theory and toy experiments suggest that these dynamics are in fact surprisingly stable. From this perspective, we hypothesise that instabilities in training GANs arise from the integration error in discretising the continuous dynamics. We experimentally verify that well-known ODE solvers (such as Runge-Kutta) can stabilise training - when combined with a regulariser that controls the integration error. Our approach represents a radical departure from previous methods which typically use adaptive optimisation and stabilisation techniques that constrain the functional space (e.g. Spectral Normalisation). Evaluation on CIFAR-10 and ImageNet shows that our method outperforms several strong baselines, demonstrating its efficacy.

Uncovering the Limits of Adversarial Training against Norm-Bounded Adversarial Examples

Adversarial training and its variants have become de facto standards for learning robust deep neural networks. In this paper, we explore the landscape around adversarial training in a bid to uncover its limits. We systematically study the effect of different training losses, model sizes, activation functions, the addition of unlabeled data (through pseudo-labeling) and other factors on adversarial robustness. We discover that it is possible to train robust models that go well beyond state-of-the-art results by combining larger models, Swish/SiLU activations and model weight averaging. We demonstrate large improvements on CIFAR-10 and CIFAR-100 against $\ell_\infty$ and $\ell_2$ norm-bounded perturbations of size $8/255$ and $128/255$, respectively. In the setting with additional unlabeled data, we obtain an accuracy under attack of 65.88% against $\ell_\infty$ perturbations of size $8/255$ on CIFAR-10 (+6.35% with respect to prior art). Without additional data, we obtain an accuracy under attack of 57.20% (+3.46%). To test the generality of our findings and without any additional modifications, we obtain an accuracy under attack of 80.53% (+7.62%) against $\ell_2$ perturbations of size $128/255$ on CIFAR-10, and of 36.88% (+8.46%) against $\ell_\infty$ perturbations of size $8/255$ on CIFAR-100.

Achieving Robustness in the Wild via Adversarial Mixing with Disentangled Representations

Recent research has made the surprising finding that state-of-the-art deep learning models sometimes fail to generalize to small variations of the input. Adversarial training has been shown to be an effective approach to overcome this problem. However, its application has been limited to enforcing invariance to analytically defined transformations like $\ell_p$-norm bounded perturbations. Such perturbations do not necessarily cover plausible real-world variations that preserve the semantics of the input (such as a change in lighting conditions). In this paper, we propose a novel approach to express and formalize robustness to these kinds of real-world transformations of the input. The two key ideas underlying our formulation are (1) leveraging disentangled representations of the input to define different factors of variations, and (2) generating new input images by adversarially composing the representations of different images. We use a StyleGAN model to demonstrate the efficacy of this framework. Specifically, we leverage the disentangled latent representations computed by a StyleGAN model to generate perturbations of an image that are similar to real-world variations (like adding make-up, or changing the skin-tone of a person) and train models to be invariant to these perturbations. Extensive experiments show that our method improves generalization and reduces the effect of spurious correlations.

An Alternative Surrogate Loss for PGD-based Adversarial Testing

Adversarial testing methods based on Projected Gradient Descent (PGD) are widely used for searching norm-bounded perturbations that cause the inputs of neural networks to be misclassified. This paper takes a deeper look at these methods and explains the effect of different hyperparameters (i.e., optimizer, step size and surrogate loss). We introduce the concept of MultiTargeted testing, which makes clever use of alternative surrogate losses, and explain when and how MultiTargeted is guaranteed to find optimal perturbations. Finally, we demonstrate that MultiTargeted outperforms more sophisticated methods and often requires less iterative steps than other variants of PGD found in the literature. Notably, MultiTargeted ranks first on MadryLab's white-box MNIST and CIFAR-10 leaderboards, reducing the accuracy of their MNIST model to 88.36% (with $\ell_\infty$ perturbations of $\epsilon = 0.3$) and the accuracy of their CIFAR-10 model to 44.03% (at $\epsilon = 8/255$). MultiTargeted also ranks first on the TRADES leaderboard reducing the accuracy of their CIFAR-10 model to 53.07% (with $\ell_\infty$ perturbations of $\epsilon = 0.031$).

Adversarial Robustness through Local Linearization

Adversarial training is an effective methodology for training deep neural networks that are robust against adversarial, norm-bounded perturbations. However, the computational cost of adversarial training grows prohibitively as the size of the model and number of input dimensions increase. Further, training against less expensive and therefore weaker adversaries produces models that are robust against weak attacks but break down under attacks that are stronger. This is often attributed to the phenomenon of gradient obfuscation; such models have a highly non-linear loss surface in the vicinity of training examples, making it hard for gradient-based attacks to succeed even though adversarial examples still exist. In this work, we introduce a novel regularizer that encourages the loss to behave linearly in the vicinity of the training data, thereby penalizing gradient obfuscation while encouraging robustness. We show via extensive experiments on CIFAR-10 and ImageNet, that models trained with our regularizer avoid gradient obfuscation and can be trained significantly faster than adversarial training. Using this regularizer, we exceed current state of the art and achieve 47% adversarial accuracy for ImageNet with l-infinity adversarial perturbations of radius 4/255 under an untargeted, strong, white-box attack. Additionally, we match state of the art results for CIFAR-10 at 8/255.

Verification of Non-Linear Specifications for Neural Networks

Prior work on neural network verification has focused on specifications that are linear functions of the output of the network, e.g., invariance of the classifier output under adversarial perturbations of the input. In this paper, we extend verification algorithms to be able to certify richer properties of neural networks. To do this we introduce the class of convex-relaxable specifications, which constitute nonlinear specifications that can be verified using a convex relaxation. We show that a number of important properties of interest can be modeled within this class, including conservation of energy in a learned dynamics model of a physical system; semantic consistency of a classifier's output labels under adversarial perturbations and bounding errors in a system that predicts the summation of handwritten digits. Our experimental evaluation shows that our method is able to effectively verify these specifications. Moreover, our evaluation exposes the failure modes in models which cannot be verified to satisfy these specifications. Thus, emphasizing the importance of training models not just to fit training data but also to be consistent with specifications.

On the Effectiveness of Interval Bound Propagation for Training Verifiably Robust Models

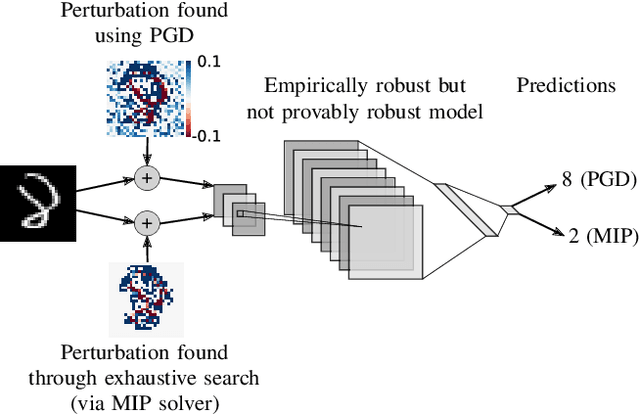
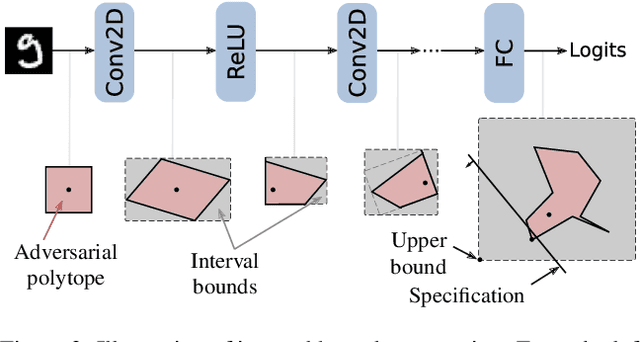
Recent works have shown that it is possible to train models that are verifiably robust to norm-bounded adversarial perturbations. While these recent methods show promise, they remain hard to scale and difficult to tune. This paper investigates how interval bound propagation (IBP) using simple interval arithmetic can be exploited to train verifiably robust neural networks that are surprisingly effective. While IBP itself has been studied in prior work, our contribution is in showing that, with an appropriate loss and careful tuning of hyper-parameters, verified training with IBP leads to a fast and stable learning algorithm. We compare our approach with recent techniques, and train classifiers that improve on the state-of-the-art in single-model adversarial robustness: we reduce the verified error rate from 3.67% to 2.23% on MNIST (with $\ell_\infty$ perturbations of $\epsilon = 0.1$), from 19.32% to 8.05% on MNIST (at $\epsilon = 0.3$), and from 78.22% to 72.91% on CIFAR-10 (at $\epsilon = 8/255$).