On the Effectiveness of Interval Bound Propagation for Training Verifiably Robust Models

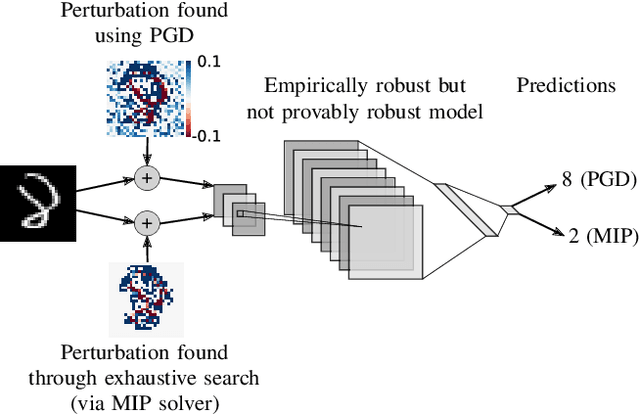
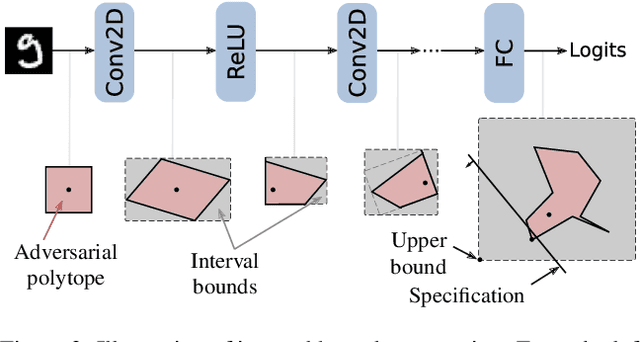
Recent works have shown that it is possible to train models that are verifiably robust to norm-bounded adversarial perturbations. While these recent methods show promise, they remain hard to scale and difficult to tune. This paper investigates how interval bound propagation (IBP) using simple interval arithmetic can be exploited to train verifiably robust neural networks that are surprisingly effective. While IBP itself has been studied in prior work, our contribution is in showing that, with an appropriate loss and careful tuning of hyper-parameters, verified training with IBP leads to a fast and stable learning algorithm. We compare our approach with recent techniques, and train classifiers that improve on the state-of-the-art in single-model adversarial robustness: we reduce the verified error rate from 3.67% to 2.23% on MNIST (with $\ell_\infty$ perturbations of $\epsilon = 0.1$), from 19.32% to 8.05% on MNIST (at $\epsilon = 0.3$), and from 78.22% to 72.91% on CIFAR-10 (at $\epsilon = 8/255$).