Adversarial vulnerability for any classifier

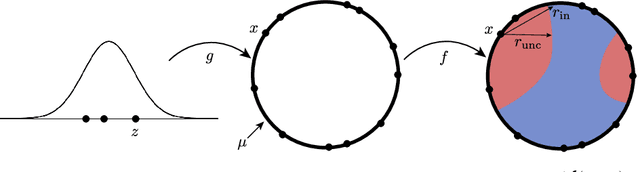
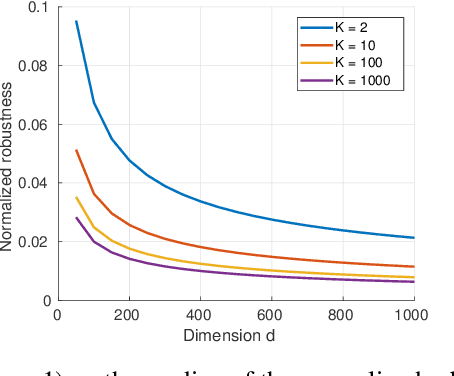
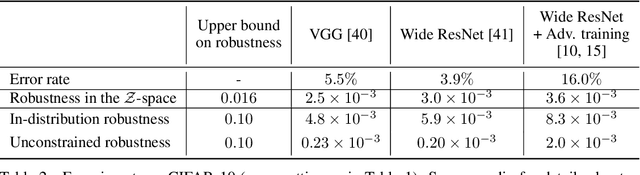
Despite achieving impressive and often superhuman performance on multiple benchmarks, state-of-the-art deep networks remain highly vulnerable to perturbations: adding small, imperceptible, adversarial perturbations can lead to very high error rates. Provided the data distribution is defined using a generative model mapping latent vectors to datapoints in the distribution, we prove that no classifier can be robust to adversarial perturbations when the latent space is sufficiently large and the generative model sufficiently smooth. Under the same conditions, we prove the existence of adversarial perturbations that transfer well across different models with small risk. We conclude the paper with experiments validating the theoretical bounds.