Small Lesion Segmentation in Brain MRIs with Subpixel Embedding

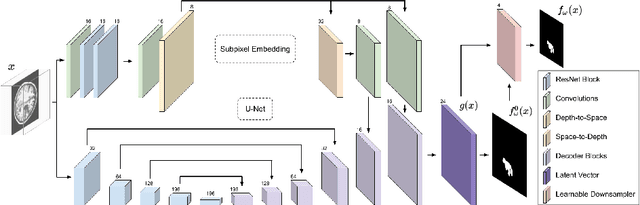
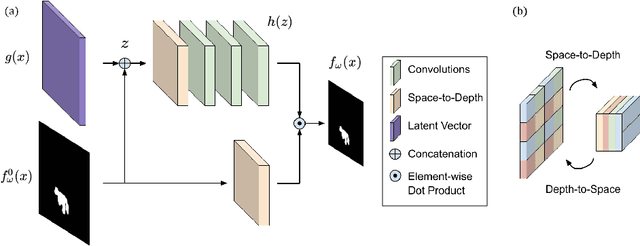
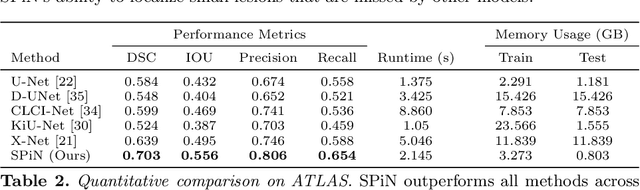
We present a method to segment MRI scans of the human brain into ischemic stroke lesion and normal tissues. We propose a neural network architecture in the form of a standard encoder-decoder where predictions are guided by a spatial expansion embedding network. Our embedding network learns features that can resolve detailed structures in the brain without the need for high-resolution training images, which are often unavailable and expensive to acquire. Alternatively, the encoder-decoder learns global structures by means of striding and max pooling. Our embedding network complements the encoder-decoder architecture by guiding the decoder with fine-grained details lost to spatial downsampling during the encoder stage. Unlike previous works, our decoder outputs at 2 times the input resolution, where a single pixel in the input resolution is predicted by four neighboring subpixels in our output. To obtain the output at the original scale, we propose a learnable downsampler (as opposed to hand-crafted ones e.g. bilinear) that combines subpixel predictions. Our approach improves the baseline architecture by approximately 11.7% and achieves the state of the art on the ATLAS public benchmark dataset with a smaller memory footprint and faster runtime than the best competing method. Our source code has been made available at: https://github.com/alexklwong/subpixel-embedding-segmentation.

Learning Topology from Synthetic Data for Unsupervised Depth Completion

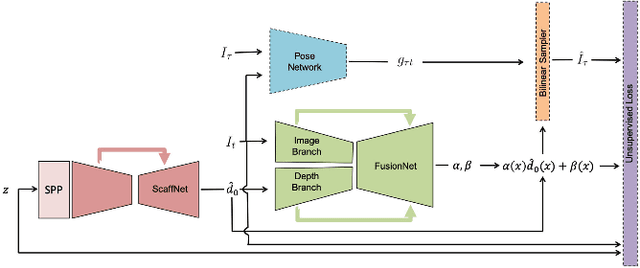
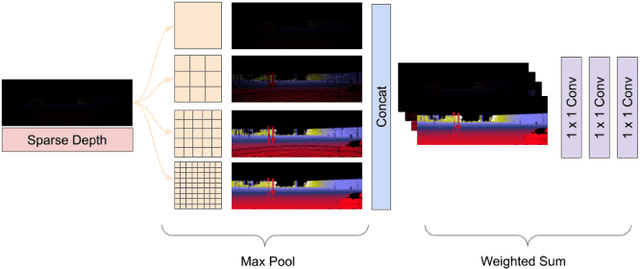
We present a method for inferring dense depth maps from images and sparse depth measurements by leveraging synthetic data to learn the association of sparse point clouds with dense natural shapes, and using the image as evidence to validate the predicted depth map. Our learned prior for natural shapes uses only sparse depth as input, not images, so the method is not affected by the covariate shift when attempting to transfer learned models from synthetic data to real ones. This allows us to use abundant synthetic data with ground truth to learn the most difficult component of the reconstruction process, which is topology estimation, and use the image to refine the prediction based on photometric evidence. Our approach uses fewer parameters than previous methods, yet, achieves the state of the art on both indoor and outdoor benchmark datasets. Code available at: https://github.com/alexklwong/learning-topology-synthetic-data.

Targeted Adversarial Perturbations for Monocular Depth Prediction

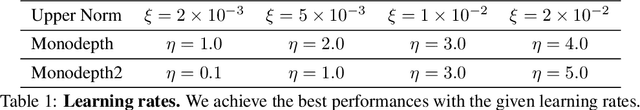
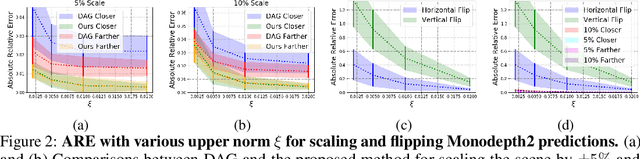
We study the effect of adversarial perturbations on the task of monocular depth prediction. Specifically, we explore the ability of small, imperceptible additive perturbations to selectively alter the perceived geometry of the scene. We show that such perturbations can not only globally re-scale the predicted distances from the camera, but also alter the prediction to match a different target scene. We also show that, when given semantic or instance information, perturbations can fool the network to alter the depth of specific categories or instances in the scene, and even remove them while preserving the rest of the scene. To understand the effect of targeted perturbations, we conduct experiments on state-of-the-art monocular depth prediction methods. Our experiments reveal vulnerabilities in monocular depth prediction networks, and shed light on the biases and context learned by them.

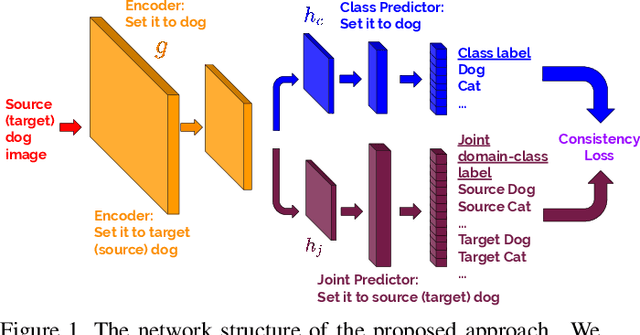
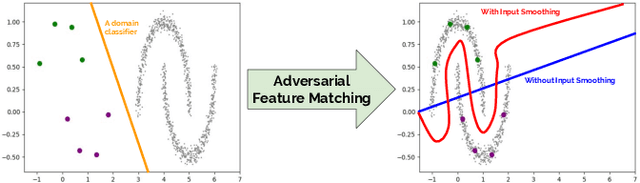
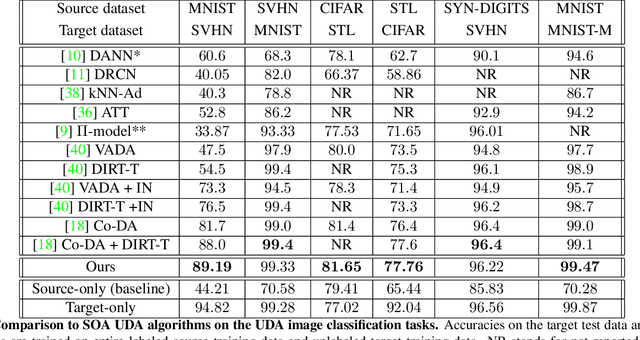
Unsupervised Domain Adaptation via Regularized Conditional Alignment

We propose a method for unsupervised domain adaptation that trains a shared embedding to align the joint distributions of inputs (domain) and outputs (classes), making any classifier agnostic to the domain. Joint alignment ensures that not only the marginal distributions of the domain are aligned, but the labels as well. We propose a novel objective function that encourages the class-conditional distributions to have disjoint support in feature space. We further exploit adversarial regularization to improve the performance of the classifier on the domain for which no annotated data is available.

Input and Weight Space Smoothing for Semi-supervised Learning

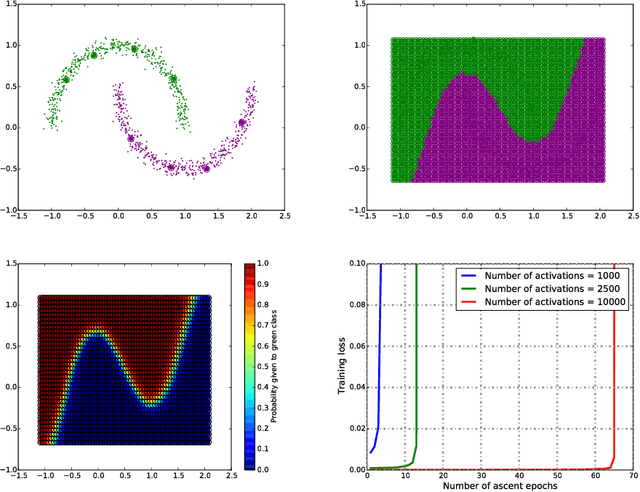
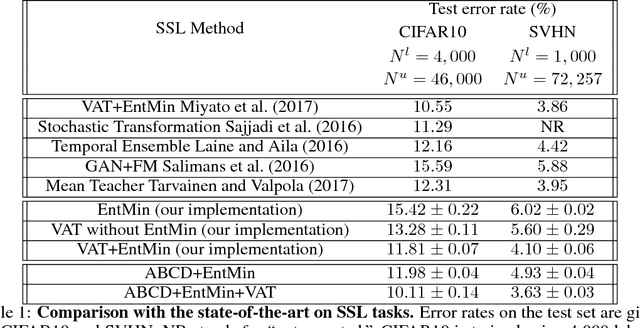
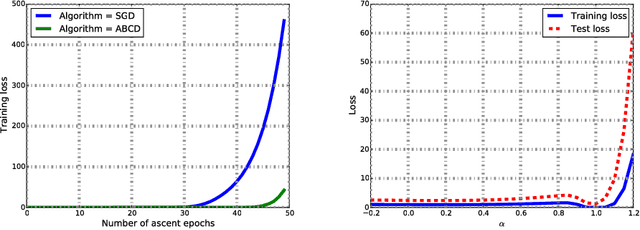
We propose regularizing the empirical loss for semi-supervised learning by acting on both the input (data) space, and the weight (parameter) space. We show that the two are not equivalent, and in fact are complementary, one affecting the minimality of the resulting representation, the other insensitivity to nuisance variability. We propose a method to perform such smoothing, which combines known input-space smoothing with a novel weight-space smoothing, based on a min-max (adversarial) optimization. The resulting Adversarial Block Coordinate Descent (ABCD) algorithm performs gradient ascent with a small learning rate for a random subset of the weights, and standard gradient descent on the remaining weights in the same mini-batch. It achieves comparable performance to the state-of-the-art without resorting to heavy data augmentation, using a relatively simple architecture.

SaaS: Speed as a Supervisor for Semi-supervised Learning

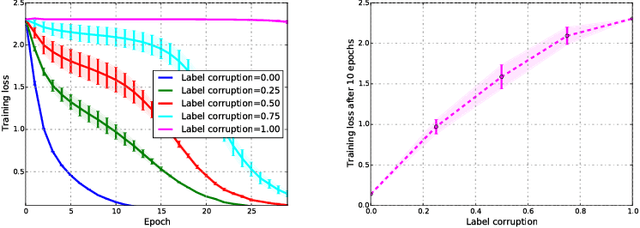
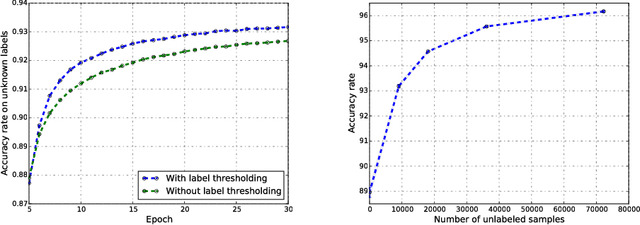
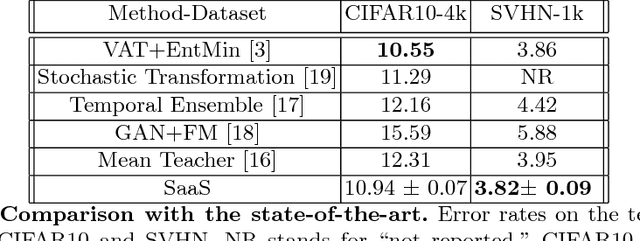
We introduce the SaaS Algorithm for semi-supervised learning, which uses learning speed during stochastic gradient descent in a deep neural network to measure the quality of an iterative estimate of the posterior probability of unknown labels. Training speed in supervised learning correlates strongly with the percentage of correct labels, so we use it as an inference criterion for the unknown labels, without attempting to infer the model parameters at first. Despite its simplicity, SaaS achieves state-of-the-art results in semi-supervised learning benchmarks.