Input and Weight Space Smoothing for Semi-supervised Learning
Paper and Code
May 23, 2018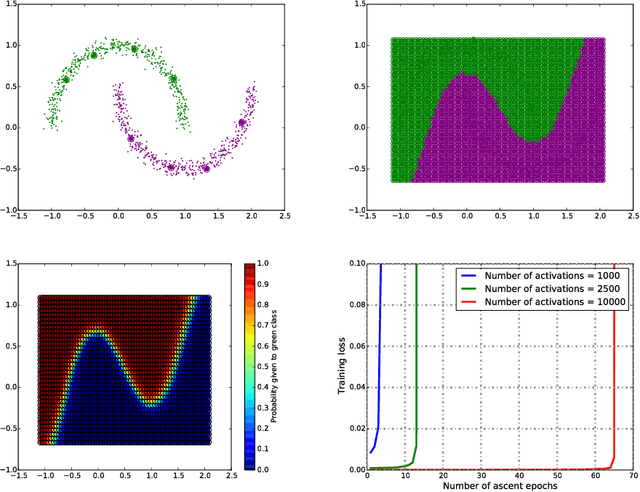
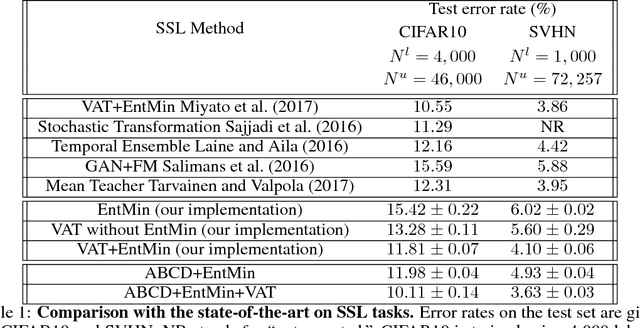
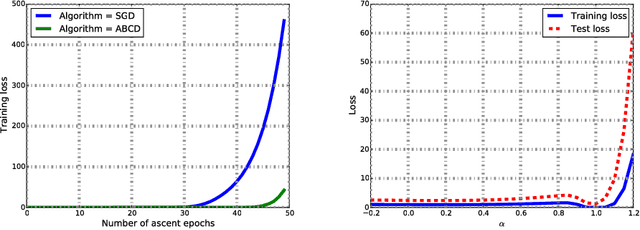
We propose regularizing the empirical loss for semi-supervised learning by acting on both the input (data) space, and the weight (parameter) space. We show that the two are not equivalent, and in fact are complementary, one affecting the minimality of the resulting representation, the other insensitivity to nuisance variability. We propose a method to perform such smoothing, which combines known input-space smoothing with a novel weight-space smoothing, based on a min-max (adversarial) optimization. The resulting Adversarial Block Coordinate Descent (ABCD) algorithm performs gradient ascent with a small learning rate for a random subset of the weights, and standard gradient descent on the remaining weights in the same mini-batch. It achieves comparable performance to the state-of-the-art without resorting to heavy data augmentation, using a relatively simple architecture.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge