Quantum learning algorithms imply circuit lower bounds

We establish the first general connection between the design of quantum algorithms and circuit lower bounds. Specifically, let $\mathfrak{C}$ be a class of polynomial-size concepts, and suppose that $\mathfrak{C}$ can be PAC-learned with membership queries under the uniform distribution with error $1/2 - \gamma$ by a time $T$ quantum algorithm. We prove that if $\gamma^2 \cdot T \ll 2^n/n$, then $\mathsf{BQE} \nsubseteq \mathfrak{C}$, where $\mathsf{BQE} = \mathsf{BQTIME}[2^{O(n)}]$ is an exponential-time analogue of $\mathsf{BQP}$. This result is optimal in both $\gamma$ and $T$, since it is not hard to learn any class $\mathfrak{C}$ of functions in (classical) time $T = 2^n$ (with no error), or in quantum time $T = \mathsf{poly}(n)$ with error at most $1/2 - \Omega(2^{-n/2})$ via Fourier sampling. In other words, even a marginal improvement on these generic learning algorithms would lead to major consequences in complexity theory. Our proof builds on several works in learning theory, pseudorandomness, and computational complexity, and crucially, on a connection between non-trivial classical learning algorithms and circuit lower bounds established by Oliveira and Santhanam (CCC 2017). Extending their approach to quantum learning algorithms turns out to create significant challenges. To achieve that, we show among other results how pseudorandom generators imply learning-to-lower-bound connections in a generic fashion, construct the first conditional pseudorandom generator secure against uniform quantum computations, and extend the local list-decoding algorithm of Impagliazzo, Jaiswal, Kabanets and Wigderson (SICOMP 2010) to quantum circuits via a delicate analysis. We believe that these contributions are of independent interest and might find other applications.

Conspiracies between Learning Algorithms, Circuit Lower Bounds and Pseudorandomness

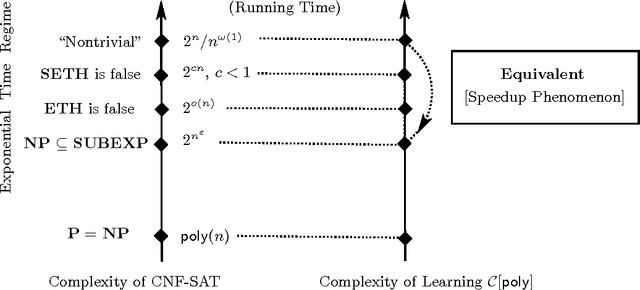
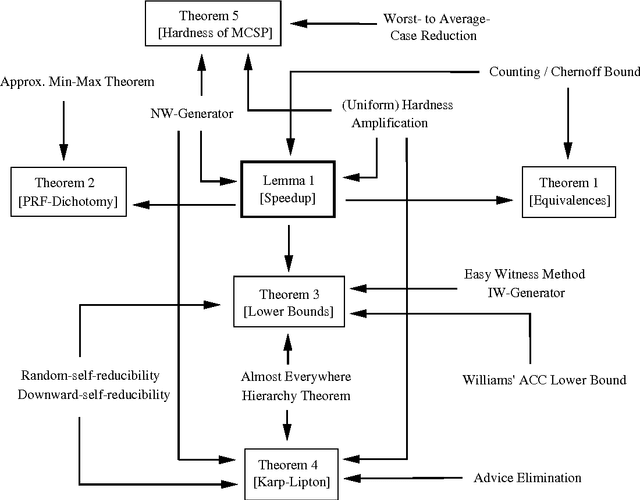
We prove several results giving new and stronger connections between learning, circuit lower bounds and pseudorandomness. Among other results, we show a generic learning speedup lemma, equivalences between various learning models in the exponential time and subexponential time regimes, a dichotomy between learning and pseudorandomness, consequences of non-trivial learning for circuit lower bounds, Karp-Lipton theorems for probabilistic exponential time, and NC$^1$-hardness for the Minimum Circuit Size Problem.

Learning circuits with few negations

Monotone Boolean functions, and the monotone Boolean circuits that compute them, have been intensively studied in complexity theory. In this paper we study the structure of Boolean functions in terms of the minimum number of negations in any circuit computing them, a complexity measure that interpolates between monotone functions and the class of all functions. We study this generalization of monotonicity from the vantage point of learning theory, giving near-matching upper and lower bounds on the uniform-distribution learnability of circuits in terms of the number of negations they contain. Our upper bounds are based on a new structural characterization of negation-limited circuits that extends a classical result of A. A. Markov. Our lower bounds, which employ Fourier-analytic tools from hardness amplification, give new results even for circuits with no negations (i.e. monotone functions).