Conspiracies between Learning Algorithms, Circuit Lower Bounds and Pseudorandomness
Paper and Code
Nov 03, 2016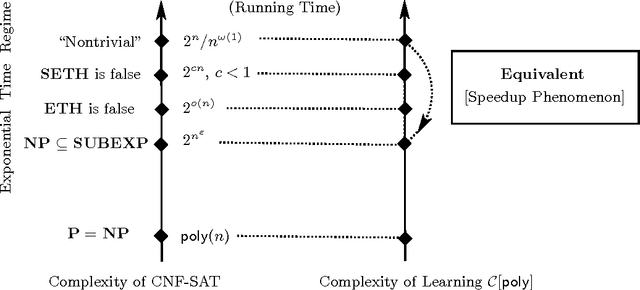
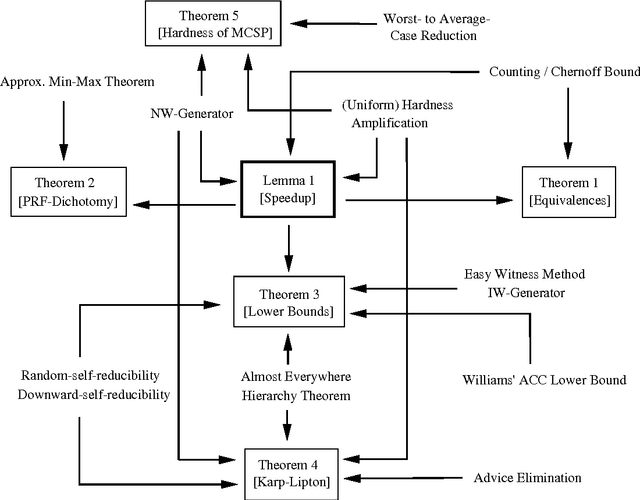
We prove several results giving new and stronger connections between learning, circuit lower bounds and pseudorandomness. Among other results, we show a generic learning speedup lemma, equivalences between various learning models in the exponential time and subexponential time regimes, a dichotomy between learning and pseudorandomness, consequences of non-trivial learning for circuit lower bounds, Karp-Lipton theorems for probabilistic exponential time, and NC$^1$-hardness for the Minimum Circuit Size Problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge