Quantum Algorithms for Reinforcement Learning with a Generative Model

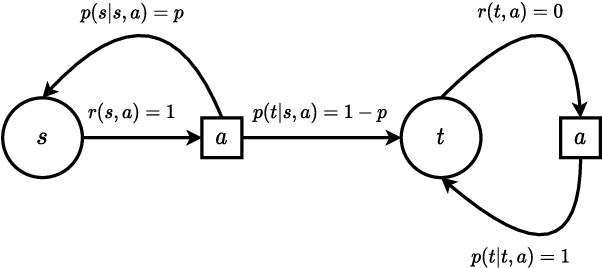
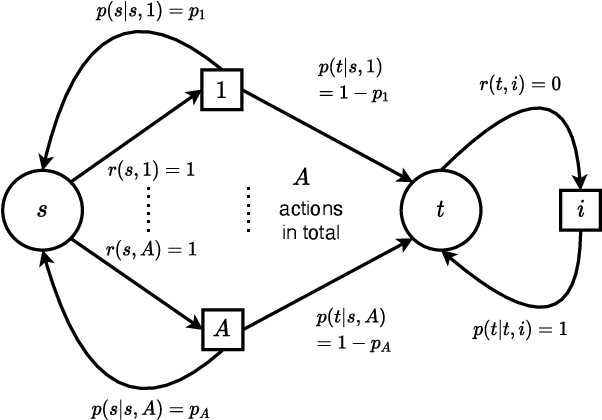
Reinforcement learning studies how an agent should interact with an environment to maximize its cumulative reward. A standard way to study this question abstractly is to ask how many samples an agent needs from the environment to learn an optimal policy for a $\gamma$-discounted Markov decision process (MDP). For such an MDP, we design quantum algorithms that approximate an optimal policy ($\pi^*$), the optimal value function ($v^*$), and the optimal $Q$-function ($q^*$), assuming the algorithms can access samples from the environment in quantum superposition. This assumption is justified whenever there exists a simulator for the environment; for example, if the environment is a video game or some other program. Our quantum algorithms, inspired by value iteration, achieve quadratic speedups over the best-possible classical sample complexities in the approximation accuracy ($\epsilon$) and two main parameters of the MDP: the effective time horizon ($\frac{1}{1-\gamma}$) and the size of the action space ($A$). Moreover, we show that our quantum algorithm for computing $q^*$ is optimal by proving a matching quantum lower bound.

Quantum learning algorithms imply circuit lower bounds

We establish the first general connection between the design of quantum algorithms and circuit lower bounds. Specifically, let $\mathfrak{C}$ be a class of polynomial-size concepts, and suppose that $\mathfrak{C}$ can be PAC-learned with membership queries under the uniform distribution with error $1/2 - \gamma$ by a time $T$ quantum algorithm. We prove that if $\gamma^2 \cdot T \ll 2^n/n$, then $\mathsf{BQE} \nsubseteq \mathfrak{C}$, where $\mathsf{BQE} = \mathsf{BQTIME}[2^{O(n)}]$ is an exponential-time analogue of $\mathsf{BQP}$. This result is optimal in both $\gamma$ and $T$, since it is not hard to learn any class $\mathfrak{C}$ of functions in (classical) time $T = 2^n$ (with no error), or in quantum time $T = \mathsf{poly}(n)$ with error at most $1/2 - \Omega(2^{-n/2})$ via Fourier sampling. In other words, even a marginal improvement on these generic learning algorithms would lead to major consequences in complexity theory. Our proof builds on several works in learning theory, pseudorandomness, and computational complexity, and crucially, on a connection between non-trivial classical learning algorithms and circuit lower bounds established by Oliveira and Santhanam (CCC 2017). Extending their approach to quantum learning algorithms turns out to create significant challenges. To achieve that, we show among other results how pseudorandom generators imply learning-to-lower-bound connections in a generic fashion, construct the first conditional pseudorandom generator secure against uniform quantum computations, and extend the local list-decoding algorithm of Impagliazzo, Jaiswal, Kabanets and Wigderson (SICOMP 2010) to quantum circuits via a delicate analysis. We believe that these contributions are of independent interest and might find other applications.

Quantum hardness of learning shallow classical circuits

In this paper we study the quantum learnability of constant-depth classical circuits under the uniform distribution and in the distribution-independent framework of PAC learning. In order to attain our results, we establish connections between quantum learning and quantum-secure cryptosystems. We then achieve the following results. 1) Hardness of learning AC$^0$ and TC$^0$ under the uniform distribution. Our first result concerns the concept class TC$^0$ (resp. AC$^0$), the class of constant-depth and polynomial-sized circuits with unbounded fan-in majority gates (resp. AND, OR, NOT gates). We show that if there exists no quantum polynomial-time (resp. sub-exponential time) algorithm to solve the Learning with Errors (LWE) problem, then there exists no polynomial-time quantum learning algorithm for TC$^0$ (resp. AC$^0$) under the uniform distribution (even with access to quantum membership queries). The main technique in this result uses explicit pseudo-random generators that are believed to be quantum-secure to construct concept classes that are hard to learn quantumly under the uniform distribution. 2) Hardness of learning TC$^0_2$ in the PAC setting. Our second result shows that if there exists no quantum polynomial time algorithm for the LWE problem, then there exists no polynomial time quantum PAC learning algorithm for the class TC$^0_2$, i.e., depth-2 TC$^0$ circuits. The main technique in this result is to establish a connection between the quantum security of public-key cryptosystems and the learnability of a concept class that consists of decryption functions of the cryptosystem. This gives a strong conditional negative answer to one of the "Ten Semi-Grand Challenges for Quantum Computing Theory" raised by Aaronson [Aar05], who asked if AC$^0$ and TC$^0$ can be PAC-learned in quantum polynomial time.