Quantum Algorithms for Reinforcement Learning with a Generative Model

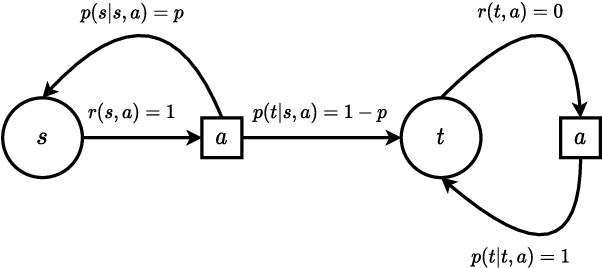
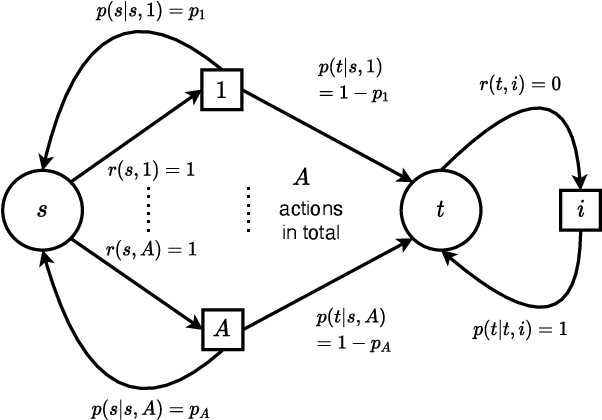
Reinforcement learning studies how an agent should interact with an environment to maximize its cumulative reward. A standard way to study this question abstractly is to ask how many samples an agent needs from the environment to learn an optimal policy for a $\gamma$-discounted Markov decision process (MDP). For such an MDP, we design quantum algorithms that approximate an optimal policy ($\pi^*$), the optimal value function ($v^*$), and the optimal $Q$-function ($q^*$), assuming the algorithms can access samples from the environment in quantum superposition. This assumption is justified whenever there exists a simulator for the environment; for example, if the environment is a video game or some other program. Our quantum algorithms, inspired by value iteration, achieve quadratic speedups over the best-possible classical sample complexities in the approximation accuracy ($\epsilon$) and two main parameters of the MDP: the effective time horizon ($\frac{1}{1-\gamma}$) and the size of the action space ($A$). Moreover, we show that our quantum algorithm for computing $q^*$ is optimal by proving a matching quantum lower bound.

Predicting human-generated bitstreams using classical and quantum models

A school of thought contends that human decision making exhibits quantum-like logic. While it is not known whether the brain may indeed be driven by actual quantum mechanisms, some researchers suggest that the decision logic is phenomenologically non-classical. This paper develops and implements an empirical framework to explore this view. We emulate binary decision-making using low width, low depth, parameterized quantum circuits. Here, entanglement serves as a resource for pattern analysis in the context of a simple bit-prediction game. We evaluate a hybrid quantum-assisted machine learning strategy where quantum processing is used to detect correlations in the bitstreams while parameter updates and class inference are performed by classical post-processing of measurement results. Simulation results indicate that a family of two-qubit variational circuits is sufficient to achieve the same bit-prediction accuracy as the best traditional classical solution such as neural nets or logistic autoregression. Thus, short of establishing a provable "quantum advantage" in this simple scenario, we give evidence that the classical predictability analysis of a human-generated bitstream can be achieved by small quantum models.

Easy and hard functions for the Boolean hidden shift problem

We study the quantum query complexity of the Boolean hidden shift problem. Given oracle access to f(x+s) for a known Boolean function f, the task is to determine the n-bit string s. The quantum query complexity of this problem depends strongly on f. We demonstrate that the easiest instances of this problem correspond to bent functions, in the sense that an exact one-query algorithm exists if and only if the function is bent. We partially characterize the hardest instances, which include delta functions. Moreover, we show that the problem is easy for random functions, since two queries suffice. Our algorithm for random functions is based on performing the pretty good measurement on several copies of a certain state; its analysis relies on the Fourier transform. We also use this approach to improve the quantum rejection sampling approach to the Boolean hidden shift problem.