Quantum Algorithms for Reinforcement Learning with a Generative Model
Paper and Code
Dec 15, 2021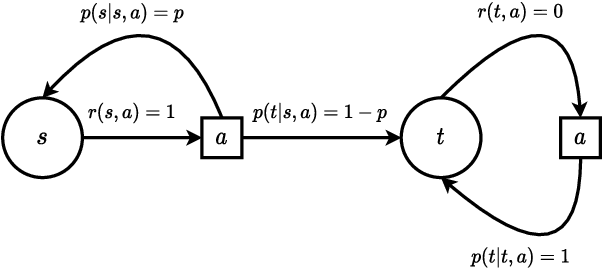
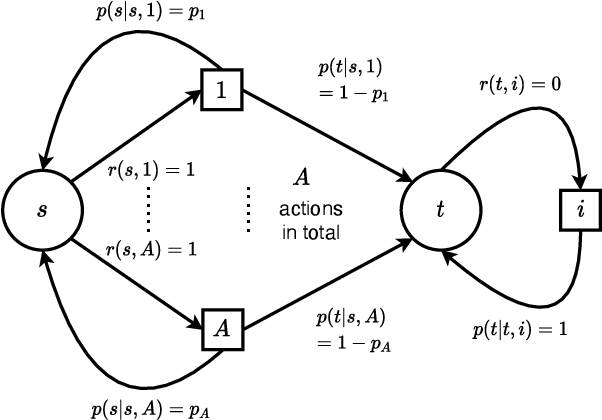
Reinforcement learning studies how an agent should interact with an environment to maximize its cumulative reward. A standard way to study this question abstractly is to ask how many samples an agent needs from the environment to learn an optimal policy for a $\gamma$-discounted Markov decision process (MDP). For such an MDP, we design quantum algorithms that approximate an optimal policy ($\pi^*$), the optimal value function ($v^*$), and the optimal $Q$-function ($q^*$), assuming the algorithms can access samples from the environment in quantum superposition. This assumption is justified whenever there exists a simulator for the environment; for example, if the environment is a video game or some other program. Our quantum algorithms, inspired by value iteration, achieve quadratic speedups over the best-possible classical sample complexities in the approximation accuracy ($\epsilon$) and two main parameters of the MDP: the effective time horizon ($\frac{1}{1-\gamma}$) and the size of the action space ($A$). Moreover, we show that our quantum algorithm for computing $q^*$ is optimal by proving a matching quantum lower bound.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge