Quantum Algorithms for Sampling Log-Concave Distributions and Estimating Normalizing Constants

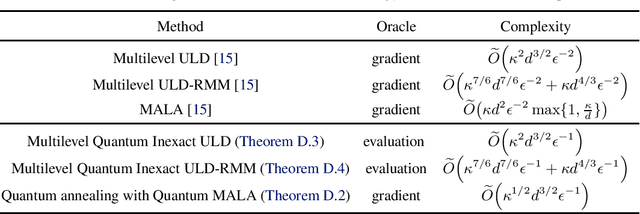
Given a convex function $f\colon\mathbb{R}^{d}\to\mathbb{R}$, the problem of sampling from a distribution $\propto e^{-f(x)}$ is called log-concave sampling. This task has wide applications in machine learning, physics, statistics, etc. In this work, we develop quantum algorithms for sampling log-concave distributions and for estimating their normalizing constants $\int_{\mathbb{R}^d}e^{-f(x)}\mathrm{d} x$. First, we use underdamped Langevin diffusion to develop quantum algorithms that match the query complexity (in terms of the condition number $\kappa$ and dimension $d$) of analogous classical algorithms that use gradient (first-order) queries, even though the quantum algorithms use only evaluation (zeroth-order) queries. For estimating normalizing constants, these algorithms also achieve quadratic speedup in the multiplicative error $\epsilon$. Second, we develop quantum Metropolis-adjusted Langevin algorithms with query complexity $\widetilde{O}(\kappa^{1/2}d)$ and $\widetilde{O}(\kappa^{1/2}d^{3/2}/\epsilon)$ for log-concave sampling and normalizing constant estimation, respectively, achieving polynomial speedups in $\kappa,d,\epsilon$ over the best known classical algorithms by exploiting quantum analogs of the Monte Carlo method and quantum walks. We also prove a $1/\epsilon^{1-o(1)}$ quantum lower bound for estimating normalizing constants, implying near-optimality of our quantum algorithms in $\epsilon$.

Quantum exploration algorithms for multi-armed bandits

Identifying the best arm of a multi-armed bandit is a central problem in bandit optimization. We study a quantum computational version of this problem with coherent oracle access to states encoding the reward probabilities of each arm as quantum amplitudes. Specifically, we show that we can find the best arm with fixed confidence using $\tilde{O}\bigl(\sqrt{\sum_{i=2}^n\Delta^{\smash{-2}}_i}\bigr)$ quantum queries, where $\Delta_{i}$ represents the difference between the mean reward of the best arm and the $i^\text{th}$-best arm. This algorithm, based on variable-time amplitude amplification and estimation, gives a quadratic speedup compared to the best possible classical result. We also prove a matching quantum lower bound (up to poly-logarithmic factors).

Easy and hard functions for the Boolean hidden shift problem

We study the quantum query complexity of the Boolean hidden shift problem. Given oracle access to f(x+s) for a known Boolean function f, the task is to determine the n-bit string s. The quantum query complexity of this problem depends strongly on f. We demonstrate that the easiest instances of this problem correspond to bent functions, in the sense that an exact one-query algorithm exists if and only if the function is bent. We partially characterize the hardest instances, which include delta functions. Moreover, we show that the problem is easy for random functions, since two queries suffice. Our algorithm for random functions is based on performing the pretty good measurement on several copies of a certain state; its analysis relies on the Fourier transform. We also use this approach to improve the quantum rejection sampling approach to the Boolean hidden shift problem.