Hypergraph Clustering Based on PageRank
Paper and Code
Jun 15, 2020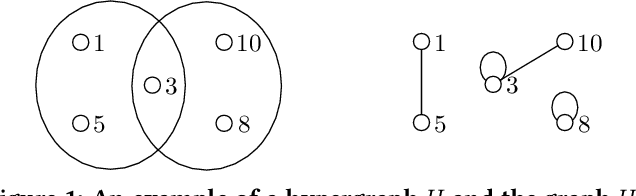
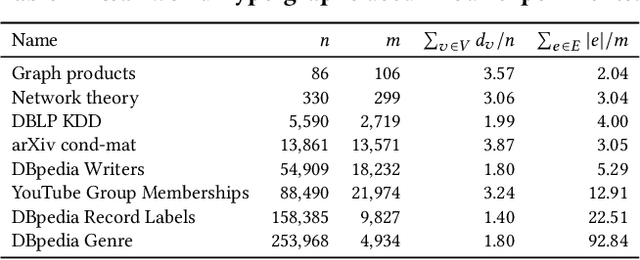
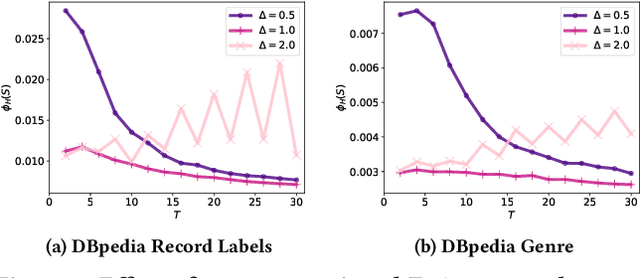
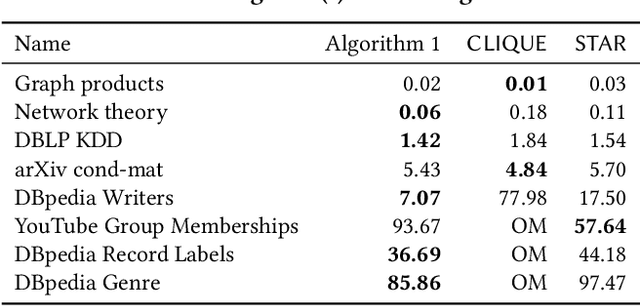
A hypergraph is a useful combinatorial object to model ternary or higher-order relations among entities. Clustering hypergraphs is a fundamental task in network analysis. In this study, we develop two clustering algorithms based on personalized PageRank on hypergraphs. The first one is local in the sense that its goal is to find a tightly connected vertex set with a bounded volume including a specified vertex. The second one is global in the sense that its goal is to find a tightly connected vertex set. For both algorithms, we discuss theoretical guarantees on the conductance of the output vertex set. Also, we experimentally demonstrate that our clustering algorithms outperform existing methods in terms of both the solution quality and running time. To the best of our knowledge, ours are the first practical algorithms for hypergraphs with theoretical guarantees on the conductance of the output set.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge