Barna Saha
Subquadratic Algorithms and Hardness for Attention with Any Temperature
May 20, 2025


Abstract:Despite the popularity of the Transformer architecture, the standard algorithm for computing Attention suffers from quadratic time complexity in context length $n$. Alman and Song [NeurIPS 2023] showed that when the head dimension $d = \Theta(\log n)$, subquadratic Attention is possible if and only if the inputs have small entries bounded by $B = o(\sqrt{\log n})$ in absolute values, under the Strong Exponential Time Hypothesis ($\mathsf{SETH}$). Equivalently, subquadratic Attention is possible if and only if the softmax is applied with high temperature for $d=\Theta(\log n)$. Running times of these algorithms depend exponentially on $B$ and thus they do not lead to even a polynomial-time algorithm outside the specific range of $B$. This naturally leads to the question: when can Attention be computed efficiently without strong assumptions on temperature? Are there fast attention algorithms that scale polylogarithmically with entry size $B$? In this work, we resolve this question and characterize when fast Attention for arbitrary temperatures is possible. First, for all constant $d = O(1)$, we give the first subquadratic $\tilde{O}(n^{2 - 1/d} \cdot \mathrm{polylog}(B))$ time algorithm for Attention with large $B$. Our result holds even for matrices with large head dimension if they have low rank. In this regime, we also give a similar running time for Attention gradient computation, and therefore for the full LLM training process. Furthermore, we show that any substantial improvement on our algorithm is unlikely. In particular, we show that even when $d = 2^{\Theta(\log^* n)}$, Attention requires $n^{2 - o(1)}$ time under $\mathsf{SETH}$. Finally, in the regime where $d = \mathrm{poly}(n)$, we show that the standard algorithm is optimal under popular fine-grained complexity assumptions.
Clustering with Non-adaptive Subset Queries
Sep 17, 2024Abstract:Recovering the underlying clustering of a set $U$ of $n$ points by asking pair-wise same-cluster queries has garnered significant interest in the last decade. Given a query $S \subset U$, $|S|=2$, the oracle returns yes if the points are in the same cluster and no otherwise. For adaptive algorithms with pair-wise queries, the number of required queries is known to be $\Theta(nk)$, where $k$ is the number of clusters. However, non-adaptive schemes require $\Omega(n^2)$ queries, which matches the trivial $O(n^2)$ upper bound attained by querying every pair of points. To break the quadratic barrier for non-adaptive queries, we study a generalization of this problem to subset queries for $|S|>2$, where the oracle returns the number of clusters intersecting $S$. Allowing for subset queries of unbounded size, $O(n)$ queries is possible with an adaptive scheme (Chakrabarty-Liao, 2024). However, the realm of non-adaptive algorithms is completely unknown. In this paper, we give the first non-adaptive algorithms for clustering with subset queries. Our main result is a non-adaptive algorithm making $O(n \log k \cdot (\log k + \log\log n)^2)$ queries, which improves to $O(n \log \log n)$ when $k$ is a constant. We also consider algorithms with a restricted query size of at most $s$. In this setting we prove that $\Omega(\max(n^2/s^2,n))$ queries are necessary and obtain algorithms making $\tilde{O}(n^2k/s^2)$ queries for any $s \leq \sqrt{n}$ and $\tilde{O}(n^2/s)$ queries for any $s \leq n$. We also consider the natural special case when the clusters are balanced, obtaining non-adaptive algorithms which make $O(n \log k) + \tilde{O}(k)$ and $O(n\log^2 k)$ queries. Finally, allowing two rounds of adaptivity, we give an algorithm making $O(n \log k)$ queries in the general case and $O(n \log \log k)$ queries when the clusters are balanced.
The I/O Complexity of Attention, or How Optimal is Flash Attention?
Feb 12, 2024Abstract:Self-attention is at the heart of the popular Transformer architecture, yet suffers from quadratic time and memory complexity. The breakthrough FlashAttention algorithm revealed I/O complexity as the true bottleneck in scaling Transformers. Given two levels of memory hierarchy, a fast cache (e.g. GPU on-chip SRAM) and a slow memory (e.g. GPU high-bandwidth memory), the I/O complexity measures the number of accesses to memory. FlashAttention computes attention using $\frac{N^2d^2}{M}$ I/O operations where $N$ is the dimension of the attention matrix, $d$ the head-dimension and $M$ the cache size. However, is this I/O complexity optimal? The known lower bound only rules out an I/O complexity of $o(Nd)$ when $M=\Theta(Nd)$, since the output that needs to be written to slow memory is $\Omega(Nd)$. This leads to the main question of our work: Is FlashAttention I/O optimal for all values of $M$? We resolve the above question in its full generality by showing an I/O complexity lower bound that matches the upper bound provided by FlashAttention for any values of $M \geq d^2$ within any constant factors. Further, we give a better algorithm with lower I/O complexity for $M < d^2$, and show that it is optimal as well. Moreover, our lower bounds do not rely on using combinatorial matrix multiplication for computing the attention matrix. We show even if one uses fast matrix multiplication, the above I/O complexity bounds cannot be improved. We do so by introducing a new communication complexity protocol for matrix compression, and connecting communication complexity to I/O complexity. To the best of our knowledge, this is the first work to establish a connection between communication complexity and I/O complexity, and we believe this connection could be of independent interest and will find many more applications in proving I/O complexity lower bounds in the future.
Community Recovery in the Geometric Block Model
Jun 22, 2022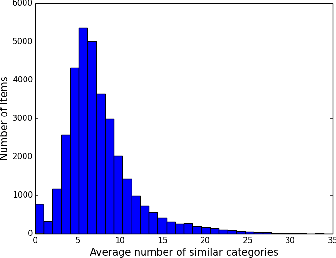
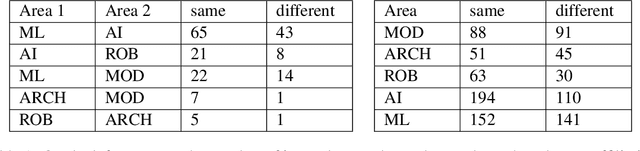
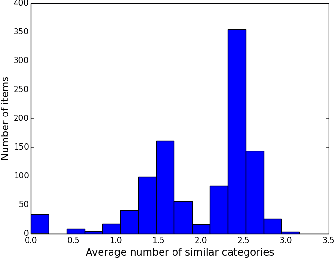

Abstract:To capture inherent geometric features of many community detection problems, we propose to use a new random graph model of communities that we call a \emph{Geometric Block Model}. The geometric block model builds on the \emph{random geometric graphs} (Gilbert, 1961), one of the basic models of random graphs for spatial networks, in the same way that the well-studied stochastic block model builds on the Erd\H{o}s-R\'{en}yi random graphs. It is also a natural extension of random community models inspired by the recent theoretical and practical advancements in community detection. To analyze the geometric block model, we first provide new connectivity results for \emph{random annulus graphs} which are generalizations of random geometric graphs. The connectivity properties of geometric graphs have been studied since their introduction, and analyzing them has been difficult due to correlated edge formation. We then use the connectivity results of random annulus graphs to provide necessary and sufficient conditions for efficient recovery of communities for the geometric block model. We show that a simple triangle-counting algorithm to detect communities in the geometric block model is near-optimal. For this we consider two regimes of graph density. In the regime where the average degree of the graph grows logarithmically with number of vertices, we show that our algorithm performs extremely well, both theoretically and practically. In contrast, the triangle-counting algorithm is far from being optimum for the stochastic block model in the logarithmic degree regime. We also look at the regime where the average degree of the graph grows linearly with the number of vertices $n$, and hence to store the graph one needs $\Theta(n^2)$ memory. We show that our algorithm needs to store only $O(n \log n)$ edges in this regime to recover the latent communities.
How to Design Robust Algorithms using Noisy Comparison Oracle
May 12, 2021
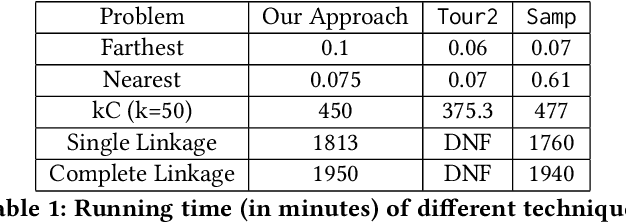
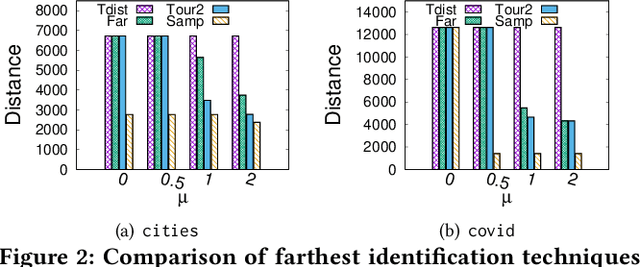
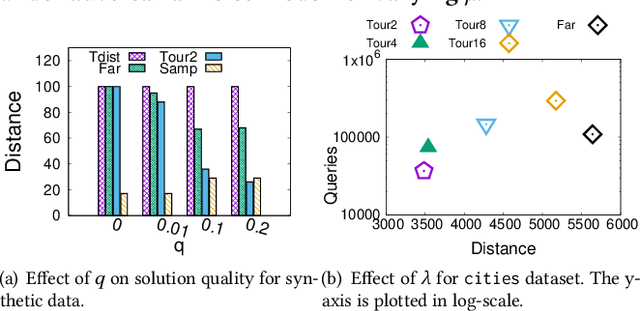
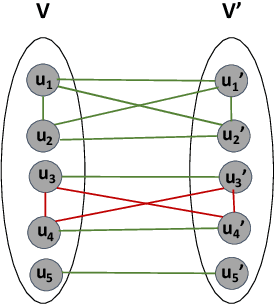
Abstract:Metric based comparison operations such as finding maximum, nearest and farthest neighbor are fundamental to studying various clustering techniques such as $k$-center clustering and agglomerative hierarchical clustering. These techniques crucially rely on accurate estimation of pairwise distance between records. However, computing exact features of the records, and their pairwise distances is often challenging, and sometimes not possible. We circumvent this challenge by leveraging weak supervision in the form of a comparison oracle that compares the relative distance between the queried points such as `Is point u closer to v or w closer to x?'. However, it is possible that some queries are easier to answer than others using a comparison oracle. We capture this by introducing two different noise models called adversarial and probabilistic noise. In this paper, we study various problems that include finding maximum, nearest/farthest neighbor search under these noise models. Building upon the techniques we develop for these comparison operations, we give robust algorithms for k-center clustering and agglomerative hierarchical clustering. We prove that our algorithms achieve good approximation guarantees with a high probability and analyze their query complexity. We evaluate the effectiveness and efficiency of our techniques empirically on various real-world datasets.
Fair Correlation Clustering
Feb 10, 2020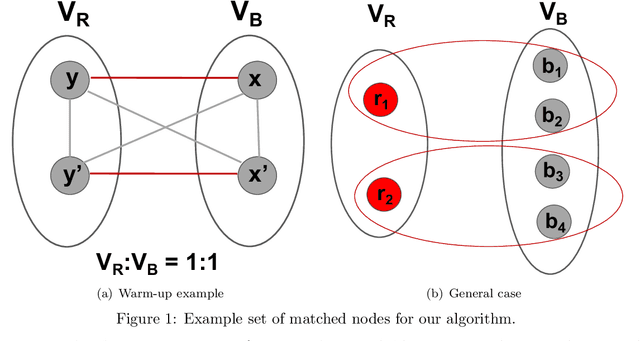


Abstract:In this paper we study the problem of correlation clustering under fairness constraints. In the classic correlation clustering problem, we are given a complete graph where each edge is labeled positive or negative. The goal is to obtain a clustering of the vertices that minimizes disagreements -- the number of negative edges trapped inside a cluster plus positive edges between different clusters. We consider two variations of fairness constraint for the problem of correlation clustering where each node has a color, and the goal is to form clusters that do not over-represent vertices of any color. The first variant aims to generate clusters with minimum disagreements, where the distribution of a feature (e.g. gender) in each cluster is same as the global distribution. For the case of two colors when the desired ratio of the number of colors in each cluster is $1:p$, we get $\mathcal{O}(p^2)$-approximation algorithm. Our algorithm could be extended to the case of multiple colors. We prove this problem is NP-hard. The second variant considers relative upper and lower bounds on the number of nodes of any color in a cluster. The goal is to avoid violating upper and lower bounds corresponding to each color in each cluster while minimizing the total number of disagreements. Along with our theoretical results, we show the effectiveness of our algorithm to generate fair clusters by empirical evaluation on real world data sets.
Correlation Clustering with Same-Cluster Queries Bounded by Optimal Cost
Aug 14, 2019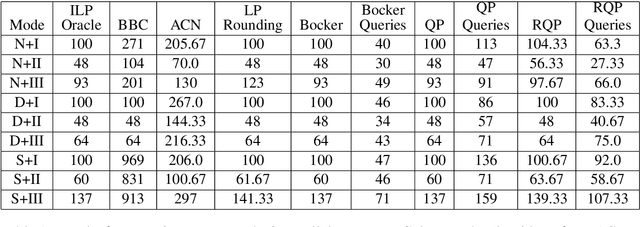

Abstract:Several clustering frameworks with interactive (semi-supervised) queries have been studied in the past. Recently, clustering with same-cluster queries has become popular. An algorithm in this setting has access to an oracle with full knowledge of an optimal clustering, and the algorithm can ask the oracle queries of the form, "Does the optimal clustering put vertices $ u $ and $ v $ in the same cluster?" Due to its simplicity, this querying model can easily be implemented in real crowd-sourcing platforms and has attracted a lot of recent work. In this paper, we study the popular correlation clustering problem (Bansal et al., 2002) under this framework. Given a complete graph $G=(V,E)$ with positive and negative edge labels, correlation clustering objective aims to compute a graph clustering that minimizes the total number of disagreements, that is the negative intra-cluster edges and positive inter-cluster edges. Let $ C_{OPT} $ be the number of disagreements made by the optimal clustering. We present algorithms for correlation clustering whose error and query bounds are parameterized by $C_{OPT}$ rather than by the number of clusters. Indeed, a good clustering must have small $C_{OPT}$. Specifically, we present an efficient algorithm that recovers an exact optimal clustering using at most $2C_{OPT} $ queries and an efficient algorithm that outputs a $2$-approximation using at most $C_{OPT} $ queries. In addition, we show under a plausible complexity assumption, there does not exist any polynomial time algorithm that has an approximation ratio better than $1+\alpha$ for an absolute constant $\alpha >0$ with $o(C_{OPT})$ queries. We extensively evaluate our methods on several synthetic and real-world datasets using real crowd-sourced oracles. Moreover, we compare our approach against several known correlation clustering algorithms.
Connectivity in Random Annulus Graphs and the Geometric Block Model
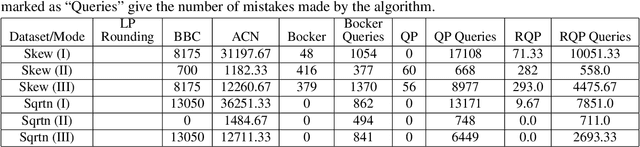
Apr 12, 2018


Abstract:Random geometric graphs are the simplest, and perhaps the earliest possible random graph model of spatial networks, introduced by Gilbert in 1961. In the most basic setting, a random geometric graph $G(n,r)$ has $n$ vertices. Each vertex of the graph is assigned a real number in $[0,1]$ randomly and uniformly. There is an edge between two vertices if the corresponding two random numbers differ by at most $r$ (to mitigate the boundary effect, let us consider the Lee distance here, $d_L(u,v) = \min\{|u-v|, 1-|u-v|\}$). It is well-known that the connectivity threshold regime for random geometric graphs is at $r \approx \frac{\log n}{n}$. In particular, if $r = \frac{a\log n}{n}$, then a random geometric graph is connected with high probability if and only if $a > 1$. Consider $G(n,\frac{(1+\epsilon)\log{n}}{n})$ for any $\epsilon >0$ to satisfy the connectivity requirement and delete half of its edges which have distance at most $\frac{\log{n}}{2n}$. It is natural to believe that the resultant graph will be disconnected. Surprisingly, we show that the graph still remains connected! Formally, generalizing random geometric graphs, we define a random annulus graph $G(n, [r_1, r_2]), r_1 <r_2$ with $n$ vertices. Each vertex of the graph is assigned a real number in $[0,1]$ randomly and uniformly as before. There is an edge between two vertices if the Lee distance between the corresponding two random numbers is between $r_1$ and $r_2$, $0<r_1<r_2$. Let us assume $r_1 = \frac{b \log n}{n},$ and $r_2 = \frac{a \log n}{n}, 0 <b <a$. We show that this graph is connected with high probability if and only if $a -b > \frac12$ and $a >1$. That is $G(n, [0,\frac{0.99\log n}{n}])$ is not connected but $G(n,[\frac{0.50 \log n}{n},\frac{1+\epsilon \log n}{n}])$ is. This result is then used to give improved lower and upper bounds on the recovery threshold of the geometric block model.
The Geometric Block Model
Jan 24, 2018
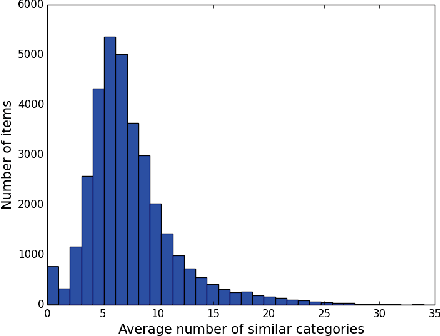
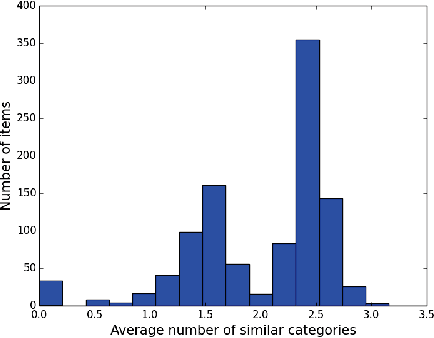

Abstract:To capture the inherent geometric features of many community detection problems, we propose to use a new random graph model of communities that we call a Geometric Block Model. The geometric block model generalizes the random geometric graphs in the same way that the well-studied stochastic block model generalizes the Erdos-Renyi random graphs. It is also a natural extension of random community models inspired by the recent theoretical and practical advancement in community detection. While being a topic of fundamental theoretical interest, our main contribution is to show that many practical community structures are better explained by the geometric block model. We also show that a simple triangle-counting algorithm to detect communities in the geometric block model is near-optimal. Indeed, even in the regime where the average degree of the graph grows only logarithmically with the number of vertices (sparse-graph), we show that this algorithm performs extremely well, both theoretically and practically. In contrast, the triangle-counting algorithm is far from being optimum for the stochastic block model. We simulate our results on both real and synthetic datasets to show superior performance of both the new model as well as our algorithm.
Query Complexity of Clustering with Side Information
Jun 23, 2017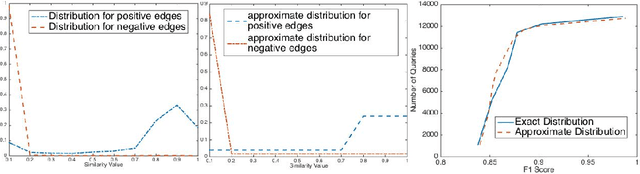
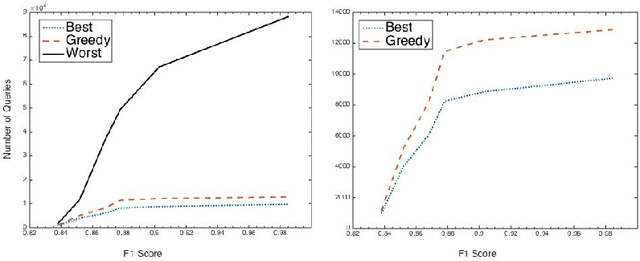
Abstract:Suppose, we are given a set of $n$ elements to be clustered into $k$ (unknown) clusters, and an oracle/expert labeler that can interactively answer pair-wise queries of the form, "do two elements $u$ and $v$ belong to the same cluster?". The goal is to recover the optimum clustering by asking the minimum number of queries. In this paper, we initiate a rigorous theoretical study of this basic problem of query complexity of interactive clustering, and provide strong information theoretic lower bounds, as well as nearly matching upper bounds. Most clustering problems come with a similarity matrix, which is used by an automated process to cluster similar points together. Our main contribution in this paper is to show the dramatic power of side information aka similarity matrix on reducing the query complexity of clustering. A similarity matrix represents noisy pair-wise relationships such as one computed by some function on attributes of the elements. A natural noisy model is where similarity values are drawn independently from some arbitrary probability distribution $f_+$ when the underlying pair of elements belong to the same cluster, and from some $f_-$ otherwise. We show that given such a similarity matrix, the query complexity reduces drastically from $\Theta(nk)$ (no similarity matrix) to $O(\frac{k^2\log{n}}{\cH^2(f_+\|f_-)})$ where $\cH^2$ denotes the squared Hellinger divergence. Moreover, this is also information-theoretic optimal within an $O(\log{n})$ factor. Our algorithms are all efficient, and parameter free, i.e., they work without any knowledge of $k, f_+$ and $f_-$, and only depend logarithmically with $n$. Along the way, our work also reveals intriguing connection to popular community detection models such as the {\em stochastic block model}, significantly generalizes them, and opens up many venues for interesting future research.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge