Correlation Clustering with Same-Cluster Queries Bounded by Optimal Cost
Paper and Code
Aug 14, 2019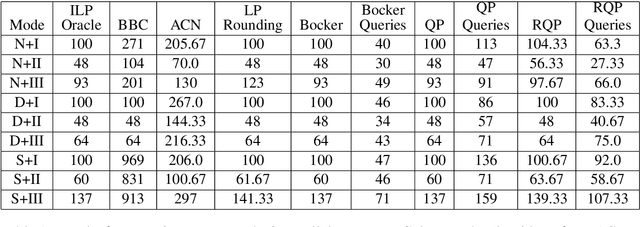
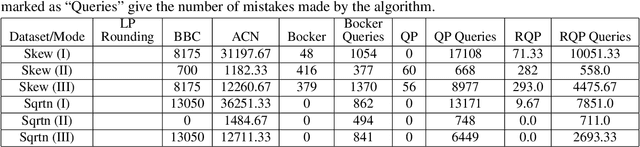

Several clustering frameworks with interactive (semi-supervised) queries have been studied in the past. Recently, clustering with same-cluster queries has become popular. An algorithm in this setting has access to an oracle with full knowledge of an optimal clustering, and the algorithm can ask the oracle queries of the form, "Does the optimal clustering put vertices $ u $ and $ v $ in the same cluster?" Due to its simplicity, this querying model can easily be implemented in real crowd-sourcing platforms and has attracted a lot of recent work. In this paper, we study the popular correlation clustering problem (Bansal et al., 2002) under this framework. Given a complete graph $G=(V,E)$ with positive and negative edge labels, correlation clustering objective aims to compute a graph clustering that minimizes the total number of disagreements, that is the negative intra-cluster edges and positive inter-cluster edges. Let $ C_{OPT} $ be the number of disagreements made by the optimal clustering. We present algorithms for correlation clustering whose error and query bounds are parameterized by $C_{OPT}$ rather than by the number of clusters. Indeed, a good clustering must have small $C_{OPT}$. Specifically, we present an efficient algorithm that recovers an exact optimal clustering using at most $2C_{OPT} $ queries and an efficient algorithm that outputs a $2$-approximation using at most $C_{OPT} $ queries. In addition, we show under a plausible complexity assumption, there does not exist any polynomial time algorithm that has an approximation ratio better than $1+\alpha$ for an absolute constant $\alpha >0$ with $o(C_{OPT})$ queries. We extensively evaluate our methods on several synthetic and real-world datasets using real crowd-sourced oracles. Moreover, we compare our approach against several known correlation clustering algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge