Connectivity in Random Annulus Graphs and the Geometric Block Model
Paper and Code
Apr 12, 2018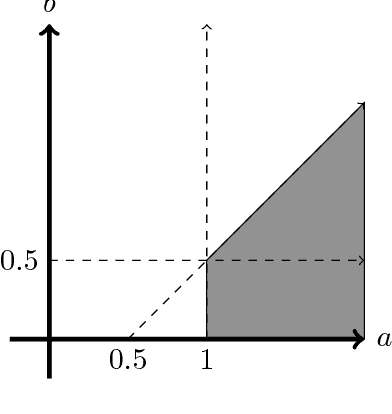


Random geometric graphs are the simplest, and perhaps the earliest possible random graph model of spatial networks, introduced by Gilbert in 1961. In the most basic setting, a random geometric graph $G(n,r)$ has $n$ vertices. Each vertex of the graph is assigned a real number in $[0,1]$ randomly and uniformly. There is an edge between two vertices if the corresponding two random numbers differ by at most $r$ (to mitigate the boundary effect, let us consider the Lee distance here, $d_L(u,v) = \min\{|u-v|, 1-|u-v|\}$). It is well-known that the connectivity threshold regime for random geometric graphs is at $r \approx \frac{\log n}{n}$. In particular, if $r = \frac{a\log n}{n}$, then a random geometric graph is connected with high probability if and only if $a > 1$. Consider $G(n,\frac{(1+\epsilon)\log{n}}{n})$ for any $\epsilon >0$ to satisfy the connectivity requirement and delete half of its edges which have distance at most $\frac{\log{n}}{2n}$. It is natural to believe that the resultant graph will be disconnected. Surprisingly, we show that the graph still remains connected! Formally, generalizing random geometric graphs, we define a random annulus graph $G(n, [r_1, r_2]), r_1 <r_2$ with $n$ vertices. Each vertex of the graph is assigned a real number in $[0,1]$ randomly and uniformly as before. There is an edge between two vertices if the Lee distance between the corresponding two random numbers is between $r_1$ and $r_2$, $0<r_1<r_2$. Let us assume $r_1 = \frac{b \log n}{n},$ and $r_2 = \frac{a \log n}{n}, 0 <b <a$. We show that this graph is connected with high probability if and only if $a -b > \frac12$ and $a >1$. That is $G(n, [0,\frac{0.99\log n}{n}])$ is not connected but $G(n,[\frac{0.50 \log n}{n},\frac{1+\epsilon \log n}{n}])$ is. This result is then used to give improved lower and upper bounds on the recovery threshold of the geometric block model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge