A Regularized Newton Method for Nonconvex Optimization with Global and Local Complexity Guarantees
Paper and Code
Feb 07, 2025
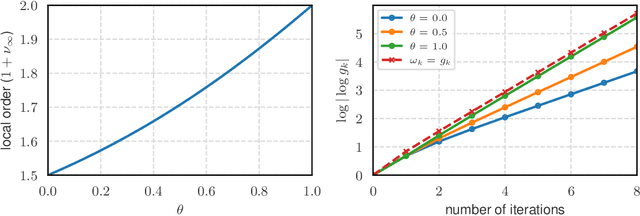
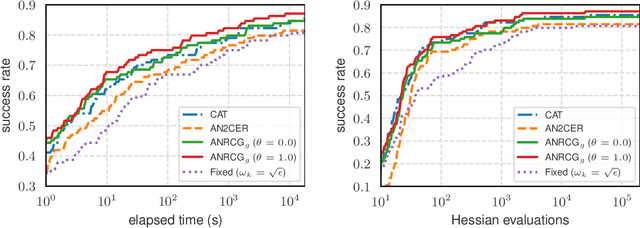
We consider the problem of finding an $\epsilon$-stationary point of a nonconvex function with a Lipschitz continuous Hessian and propose a quadratic regularized Newton method incorporating a new class of regularizers constructed from the current and previous gradients. The method leverages a recently developed linear conjugate gradient approach with a negative curvature monitor to solve the regularized Newton equation. Notably, our algorithm is adaptive, requiring no prior knowledge of the Lipschitz constant of the Hessian, and achieves a global complexity of $O(\epsilon^{-\frac{3}{2}}) + \tilde O(1)$ in terms of the second-order oracle calls, and $\tilde O(\epsilon^{-\frac{7}{4}})$ for Hessian-vector products, respectively. Moreover, when the iterates converge to a point where the Hessian is positive definite, the method exhibits quadratic local convergence. Preliminary numerical results illustrate the competitiveness of our algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge