Revealing hidden dynamics from time-series data by ODENet

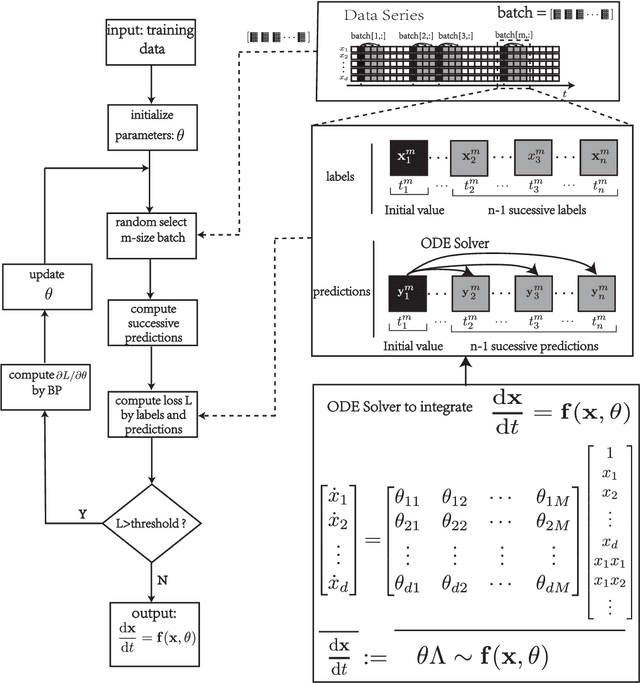
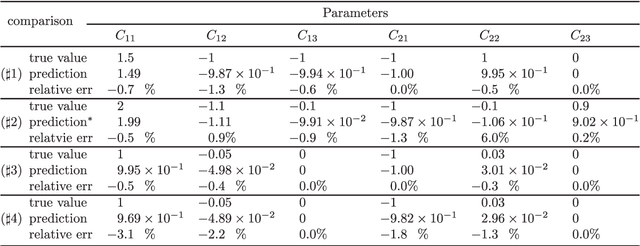
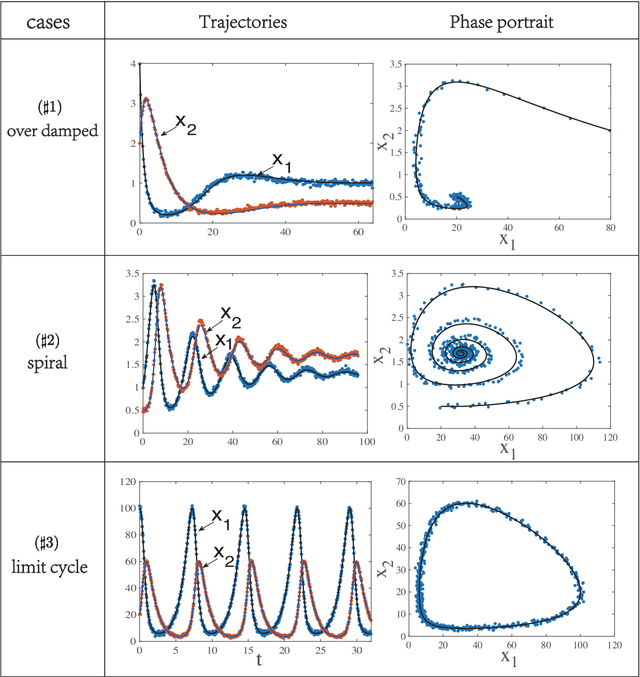
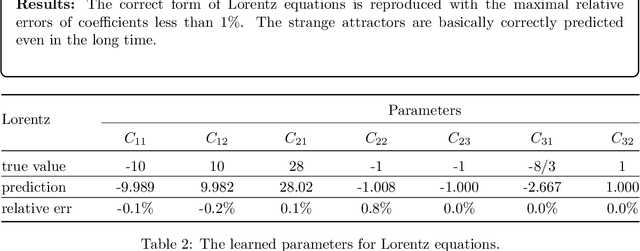
To understand the hidden physical concepts from observed data is the most basic but challenging problem in many fields. In this study, we propose a new type of interpretable neural network called the ordinary differential equation network (ODENet) to reveal the hidden dynamics buried in the massive time-series data. Specifically, we construct explicit models presented by ordinary differential equations (ODEs) to describe the observed data without any prior knowledge. In contrast to other previous neural networks which are black boxes for users, the ODENet in this work is an imitation of the difference scheme for ODEs, with each step computed by an ODE solver, and thus is completely understandable. Backpropagation algorithms are used to update the coefficients of a group of orthogonal basis functions, which specify the concrete form of ODEs, under the guidance of loss function with sparsity requirement. From classical Lotka-Volterra equations to chaotic Lorenz equations, the ODENet demonstrates its remarkable capability to deal with time-series data. In the end, we apply the ODENet to real actin aggregation data observed by experimentalists, and it shows an impressive performance as well.