MEP-Net: Generating Solutions to Scientific Problems with Limited Knowledge by Maximum Entropy Principle

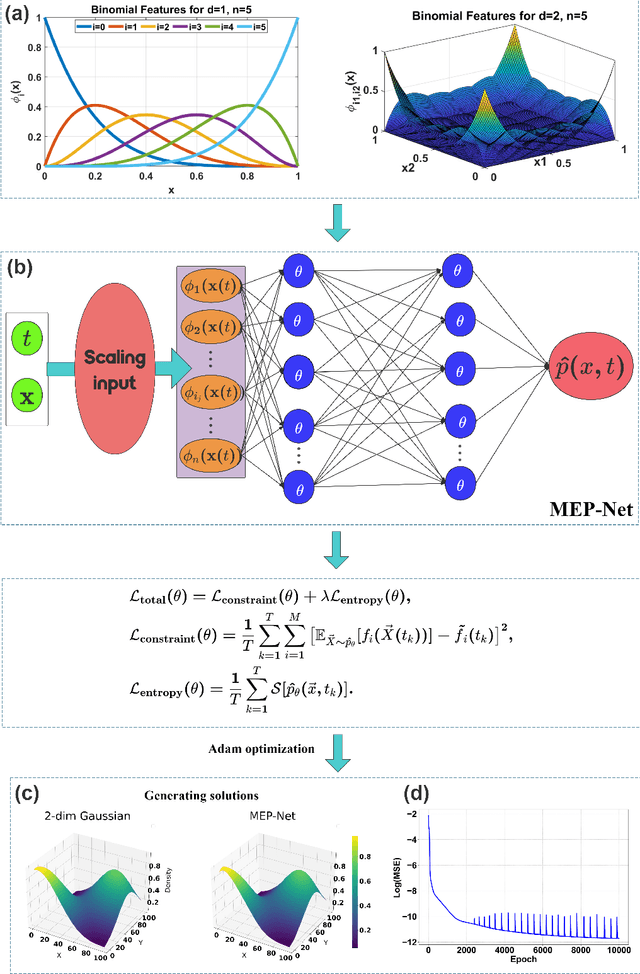
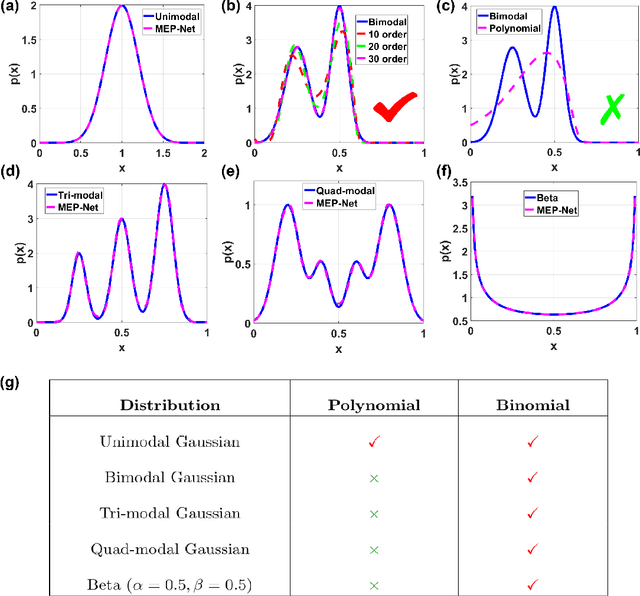
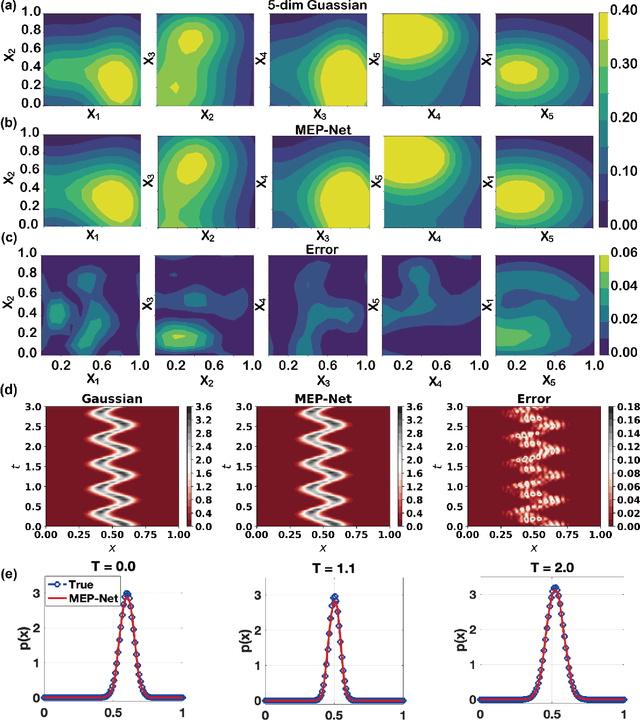
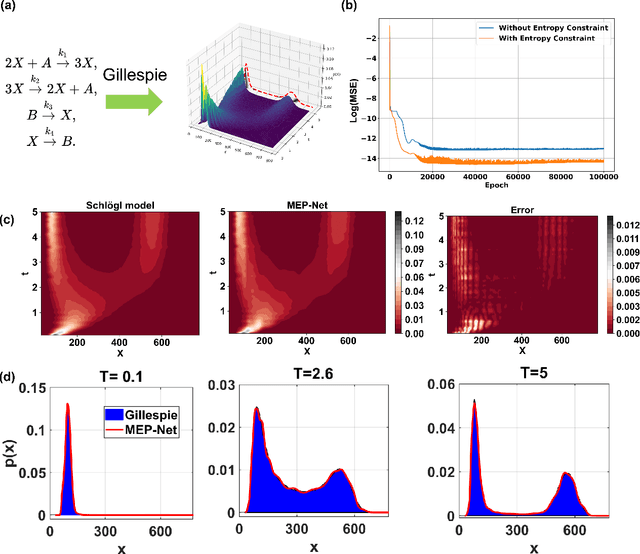
Maximum entropy principle (MEP) offers an effective and unbiased approach to inferring unknown probability distributions when faced with incomplete information, while neural networks provide the flexibility to learn complex distributions from data. This paper proposes a novel neural network architecture, the MEP-Net, which combines the MEP with neural networks to generate probability distributions from moment constraints. We also provide a comprehensive overview of the fundamentals of the maximum entropy principle, its mathematical formulations, and a rigorous justification for its applicability for non-equilibrium systems based on the large deviations principle. Through fruitful numerical experiments, we demonstrate that the MEP-Net can be particularly useful in modeling the evolution of probability distributions in biochemical reaction networks and in generating complex distributions from data.

Identification of hydrodynamic instability by convolutional neural networks

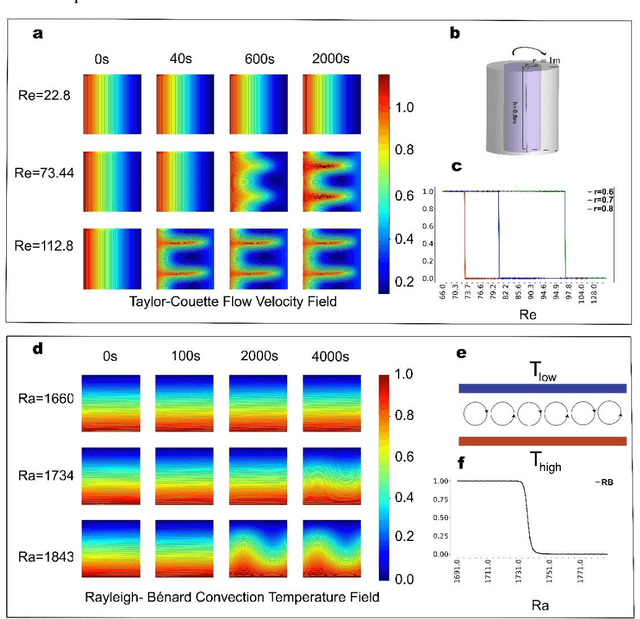
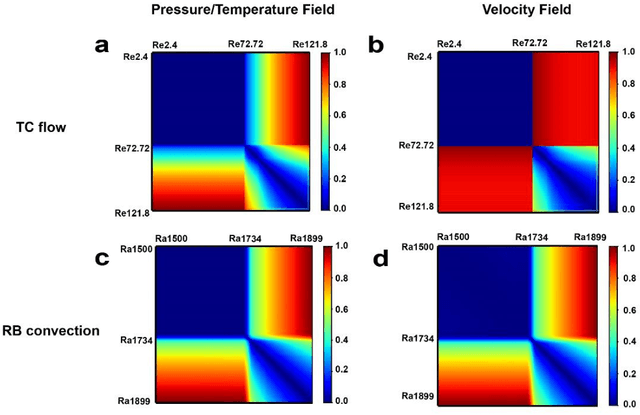
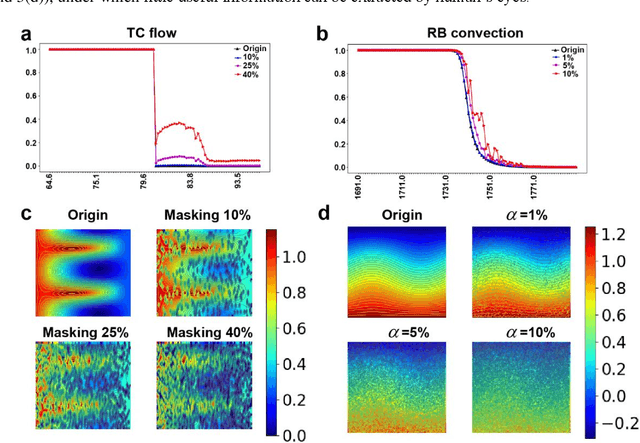
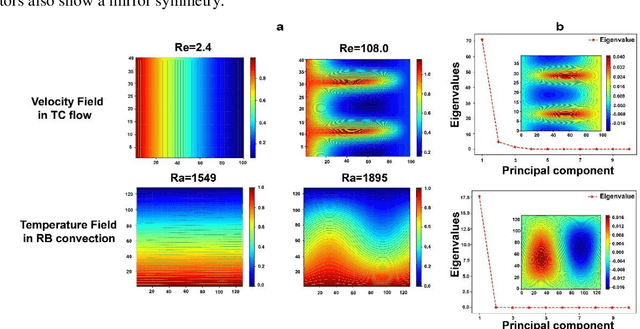
The onset of hydrodynamic instabilities is of great importance in both industry and daily life, due to the dramatic mechanical and thermodynamic changes for different types of flow motions. In this paper, modern machine learning techniques, especially the convolutional neural networks (CNN), are applied to identify the transition between different flow motions raised by hydrodynamic instability, as well as critical non-dimensionalized parameters for characterizing this transit. CNN not only correctly predicts the critical transition values for both Taylor-Couette (TC) flow and Rayleigh- B\'enard (RB) convection under various setups and conditions, but also shows an outstanding performance on robustness and noise-tolerance. In addition, key spatial features used for classifying different flow patterns are revealed by the principal component analysis.

When Machine Learning Meets Multiscale Modeling in Chemical Reactions

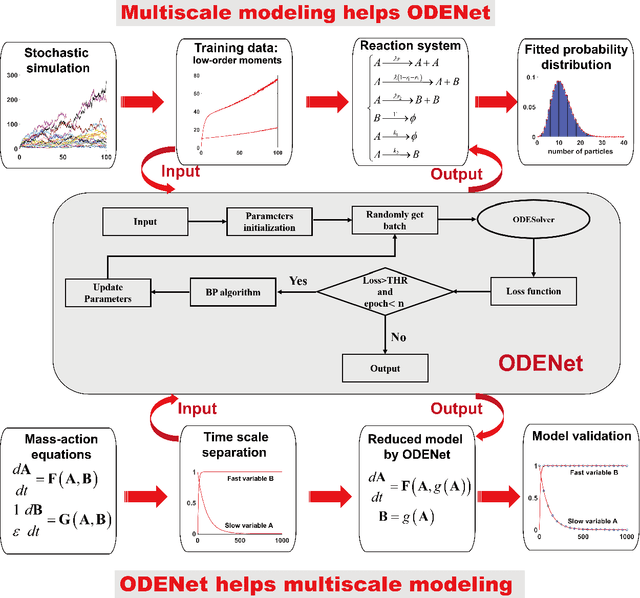
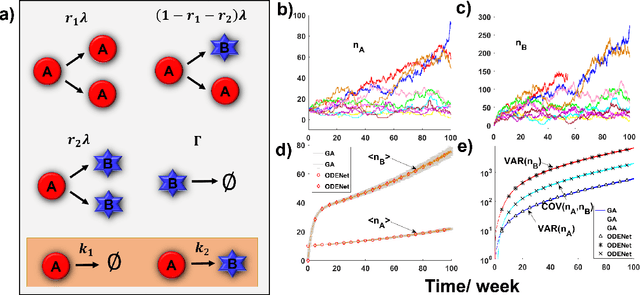
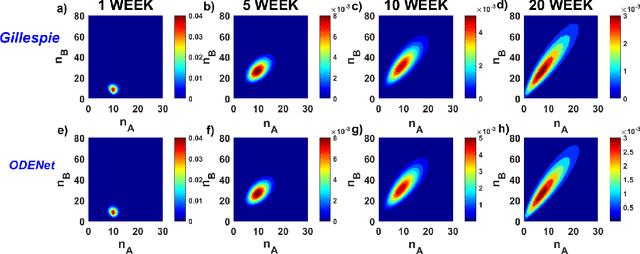
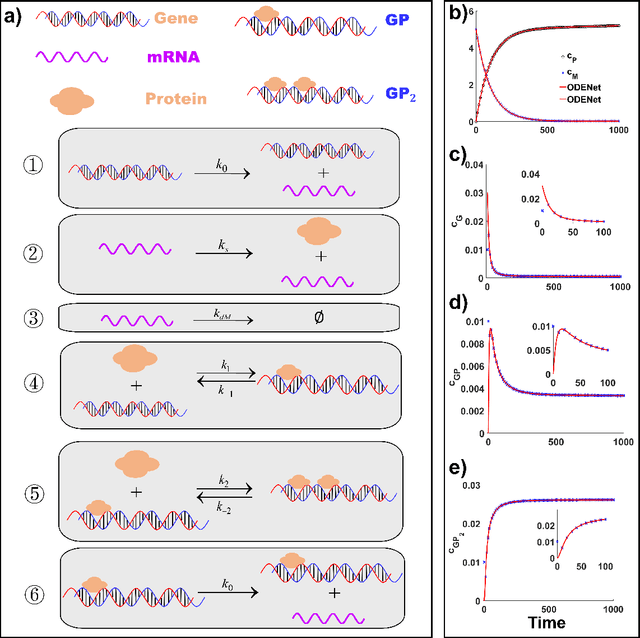
Due to the intrinsic complexity and nonlinearity of chemical reactions, direct applications of traditional machine learning algorithms may face with many difficulties. In this study, through two concrete examples with biological background, we illustrate how the key ideas of multiscale modeling can help to reduce the computational cost of machine learning a lot, as well as how machine learning algorithms perform model reduction automatically in a time-scale separated system. Our study highlights the necessity and effectiveness of an integration of machine learning algorithms and multiscale modeling during the study of chemical reactions.

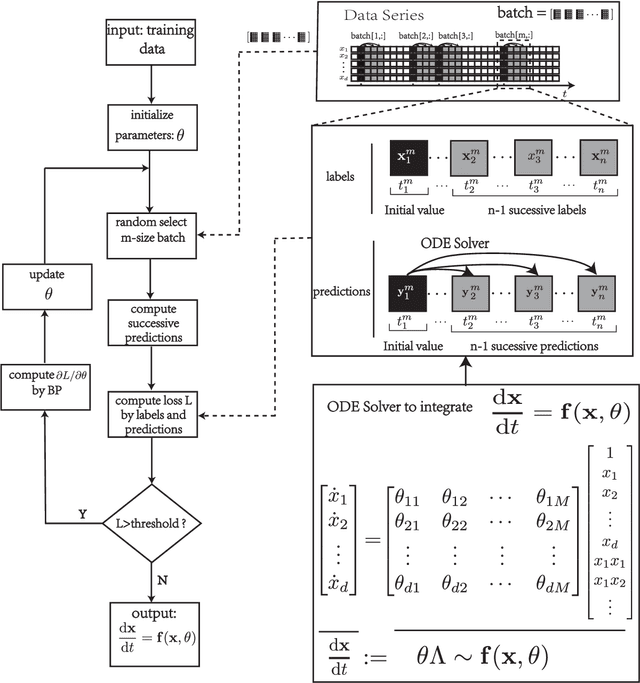
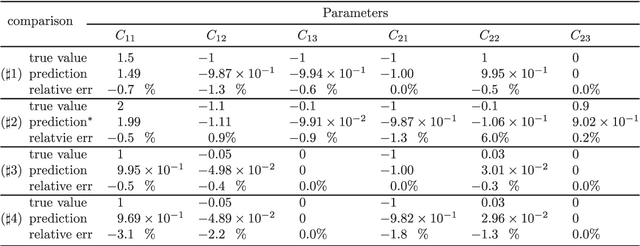
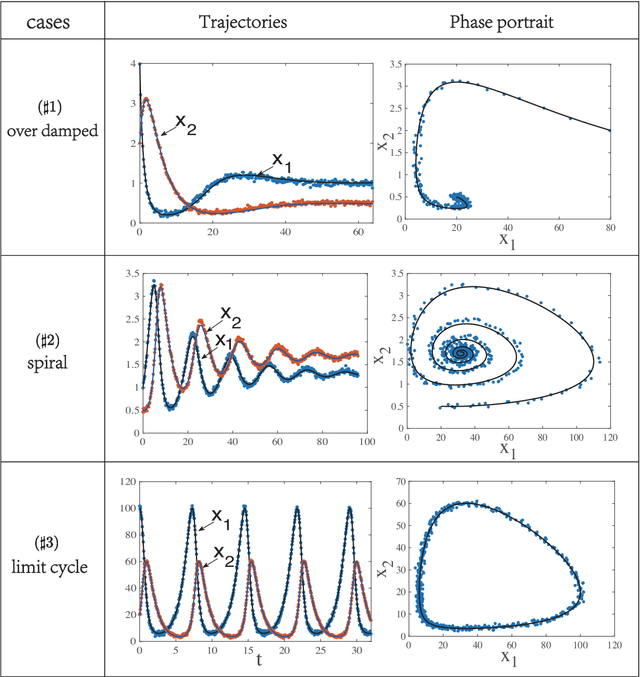
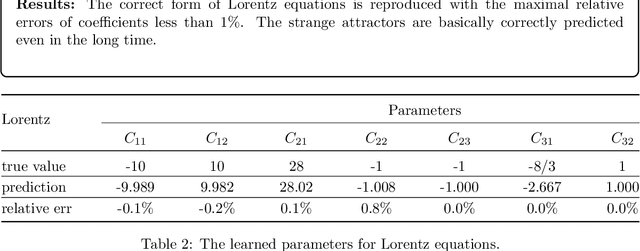
Revealing hidden dynamics from time-series data by ODENet

To understand the hidden physical concepts from observed data is the most basic but challenging problem in many fields. In this study, we propose a new type of interpretable neural network called the ordinary differential equation network (ODENet) to reveal the hidden dynamics buried in the massive time-series data. Specifically, we construct explicit models presented by ordinary differential equations (ODEs) to describe the observed data without any prior knowledge. In contrast to other previous neural networks which are black boxes for users, the ODENet in this work is an imitation of the difference scheme for ODEs, with each step computed by an ODE solver, and thus is completely understandable. Backpropagation algorithms are used to update the coefficients of a group of orthogonal basis functions, which specify the concrete form of ODEs, under the guidance of loss function with sparsity requirement. From classical Lotka-Volterra equations to chaotic Lorenz equations, the ODENet demonstrates its remarkable capability to deal with time-series data. In the end, we apply the ODENet to real actin aggregation data observed by experimentalists, and it shows an impressive performance as well.