MEP-Net: Generating Solutions to Scientific Problems with Limited Knowledge by Maximum Entropy Principle
Paper and Code
Dec 03, 2024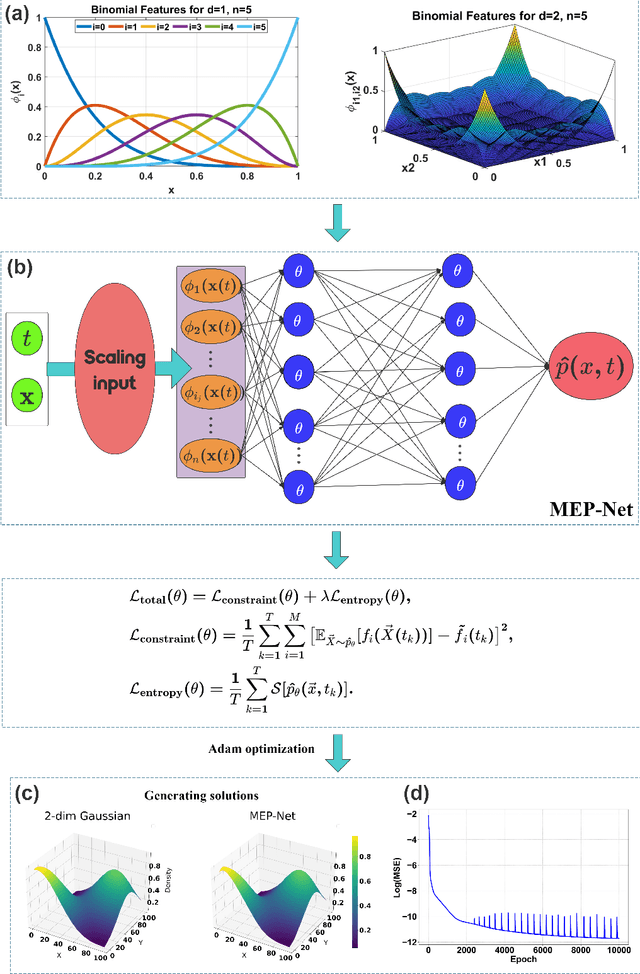
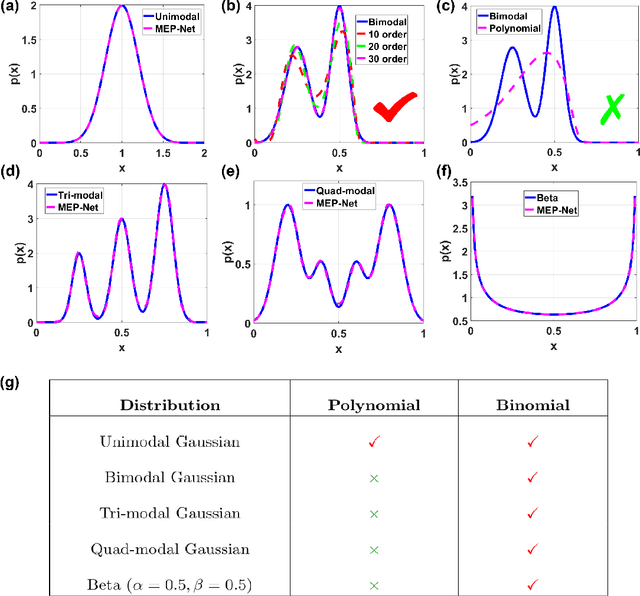
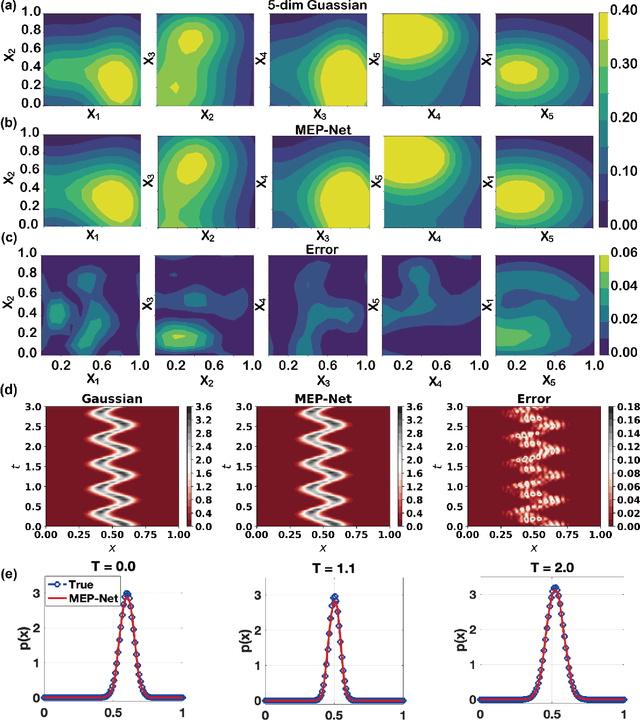
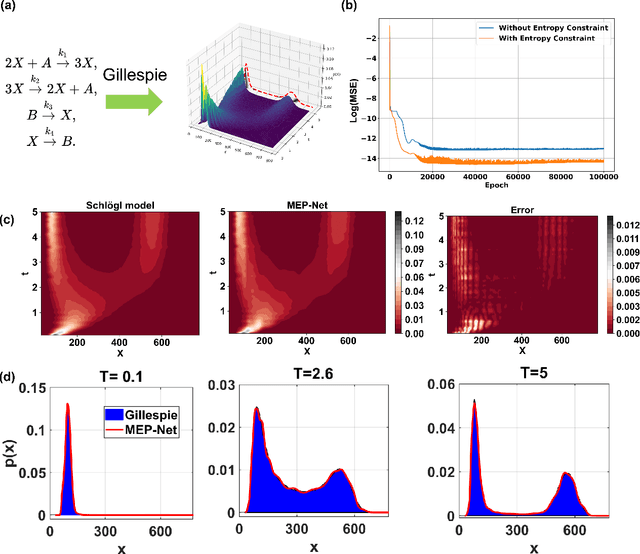
Maximum entropy principle (MEP) offers an effective and unbiased approach to inferring unknown probability distributions when faced with incomplete information, while neural networks provide the flexibility to learn complex distributions from data. This paper proposes a novel neural network architecture, the MEP-Net, which combines the MEP with neural networks to generate probability distributions from moment constraints. We also provide a comprehensive overview of the fundamentals of the maximum entropy principle, its mathematical formulations, and a rigorous justification for its applicability for non-equilibrium systems based on the large deviations principle. Through fruitful numerical experiments, we demonstrate that the MEP-Net can be particularly useful in modeling the evolution of probability distributions in biochemical reaction networks and in generating complex distributions from data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge