Learning Adversarial Low-rank Markov Decision Processes with Unknown Transition and Full-information Feedback

In this work, we study the low-rank MDPs with adversarially changed losses in the full-information feedback setting. In particular, the unknown transition probability kernel admits a low-rank matrix decomposition \citep{REPUCB22}, and the loss functions may change adversarially but are revealed to the learner at the end of each episode. We propose a policy optimization-based algorithm POLO, and we prove that it attains the $\widetilde{O}(K^{\frac{5}{6}}A^{\frac{1}{2}}d\ln(1+M)/(1-\gamma)^2)$ regret guarantee, where $d$ is rank of the transition kernel (and hence the dimension of the unknown representations), $A$ is the cardinality of the action space, $M$ is the cardinality of the model class, and $\gamma$ is the discounted factor. Notably, our algorithm is oracle-efficient and has a regret guarantee with no dependence on the size of potentially arbitrarily large state space. Furthermore, we also prove an $\Omega(\frac{\gamma^2}{1-\gamma} \sqrt{d A K})$ regret lower bound for this problem, showing that low-rank MDPs are statistically more difficult to learn than linear MDPs in the regret minimization setting. To the best of our knowledge, we present the first algorithm that interleaves representation learning, exploration, and exploitation to achieve the sublinear regret guarantee for RL with nonlinear function approximation and adversarial losses.

DPMAC: Differentially Private Communication for Cooperative Multi-Agent Reinforcement Learning

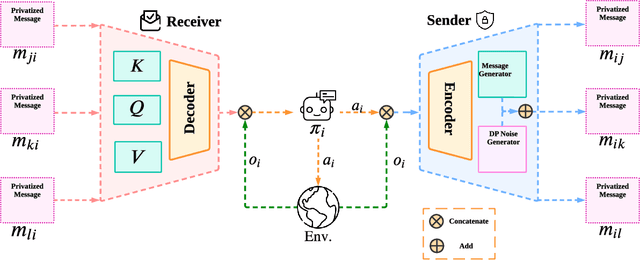
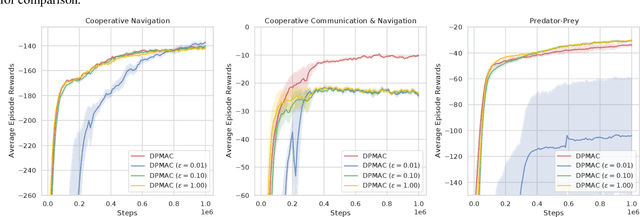
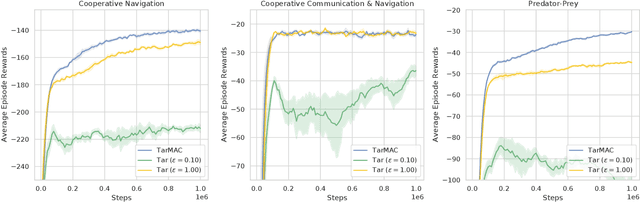
Communication lays the foundation for cooperation in human society and in multi-agent reinforcement learning (MARL). Humans also desire to maintain their privacy when communicating with others, yet such privacy concern has not been considered in existing works in MARL. To this end, we propose the \textit{differentially private multi-agent communication} (DPMAC) algorithm, which protects the sensitive information of individual agents by equipping each agent with a local message sender with rigorous $(\epsilon, \delta)$-differential privacy (DP) guarantee. In contrast to directly perturbing the messages with predefined DP noise as commonly done in privacy-preserving scenarios, we adopt a stochastic message sender for each agent respectively and incorporate the DP requirement into the sender, which automatically adjusts the learned message distribution to alleviate the instability caused by DP noise. Further, we prove the existence of a Nash equilibrium in cooperative MARL with privacy-preserving communication, which suggests that this problem is game-theoretically learnable. Extensive experiments demonstrate a clear advantage of DPMAC over baseline methods in privacy-preserving scenarios.

Best-of-three-worlds Analysis for Linear Bandits with Follow-the-regularized-leader Algorithm

The linear bandit problem has been studied for many years in both stochastic and adversarial settings. Designing an algorithm that can optimize the environment without knowing the loss type attracts lots of interest. \citet{LeeLWZ021} propose an algorithm that actively detects the loss type and then switches between different algorithms specially designed for different settings. However, such an approach requires meticulous designs to perform well in all settings. Follow-the-regularized-leader (FTRL) is another popular algorithm type that can adapt to different environments. This algorithm is of simple design and the regret bounds are shown to be optimal in traditional multi-armed bandit problems compared with the detect-switch type algorithms. Designing an FTRL-type algorithm for linear bandits is an important question that has been open for a long time. In this paper, we prove that the FTRL-type algorithm with a negative entropy regularizer can achieve the best-of-three-world results for the linear bandit problem with the tacit cooperation between the choice of the learning rate and the specially designed self-bounding inequality.

Comparison-based Conversational Recommender System with Relative Bandit Feedback

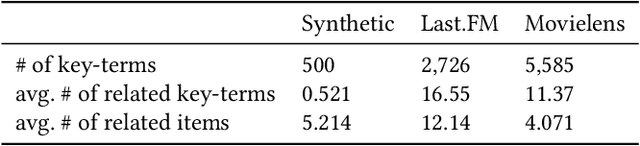
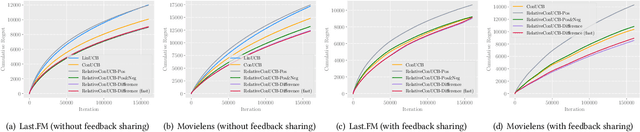
With the recent advances of conversational recommendations, the recommender system is able to actively and dynamically elicit user preference via conversational interactions. To achieve this, the system periodically queries users' preference on attributes and collects their feedback. However, most existing conversational recommender systems only enable the user to provide absolute feedback to the attributes. In practice, the absolute feedback is usually limited, as the users tend to provide biased feedback when expressing the preference. Instead, the user is often more inclined to express comparative preferences, since user preferences are inherently relative. To enable users to provide comparative preferences during conversational interactions, we propose a novel comparison-based conversational recommender system. The relative feedback, though more practical, is not easy to be incorporated since its feedback scale is always mismatched with users' absolute preferences. With effectively collecting and understanding the relative feedback from an interactive manner, we further propose a new bandit algorithm, which we call RelativeConUCB. The experiments on both synthetic and real-world datasets validate the advantage of our proposed method, compared to the existing bandit algorithms in the conversational recommender systems.

Simultaneously Learning Stochastic and Adversarial Bandits under the Position-Based Model

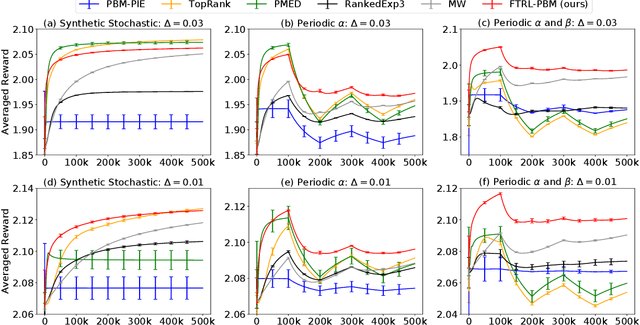
Online learning to rank (OLTR) interactively learns to choose lists of items from a large collection based on certain click models that describe users' click behaviors. Most recent works for this problem focus on the stochastic environment where the item attractiveness is assumed to be invariant during the learning process. In many real-world scenarios, however, the environment could be dynamic or even arbitrarily changing. This work studies the OLTR problem in both stochastic and adversarial environments under the position-based model (PBM). We propose a method based on the follow-the-regularized-leader (FTRL) framework with Tsallis entropy and develop a new self-bounding constraint especially designed for PBM. We prove the proposed algorithm simultaneously achieves $O(\log{T})$ regret in the stochastic environment and $O(m\sqrt{nT})$ regret in the adversarial environment, where $T$ is the number of rounds, $n$ is the number of items and $m$ is the number of positions. We also provide a lower bound of order $\Omega(m\sqrt{nT})$ for adversarial PBM, which matches our upper bound and improves over the state-of-the-art lower bound. The experiments show that our algorithm could simultaneously learn in both stochastic and adversarial environments and is competitive compared to existing methods that are designed for a single environment.

Differentially Private Temporal Difference Learning with Stochastic Nonconvex-Strongly-Concave Optimization

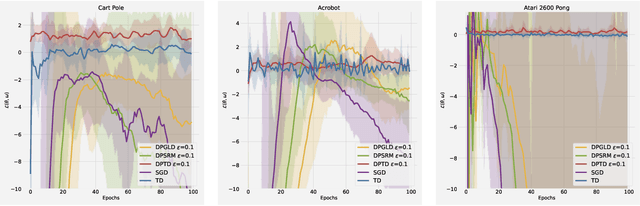
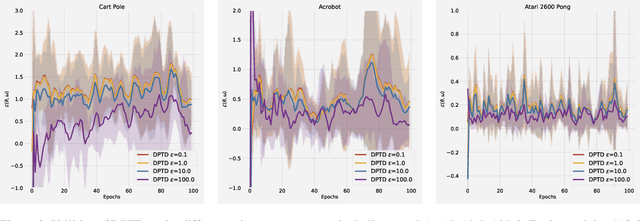
Temporal difference (TD) learning is a widely used method to evaluate policies in reinforcement learning. While many TD learning methods have been developed in recent years, little attention has been paid to preserving privacy and most of the existing approaches might face the concerns of data privacy from users. To enable complex representative abilities of policies, in this paper, we consider preserving privacy in TD learning with nonlinear value function approximation. This is challenging because such a nonlinear problem is usually studied in the formulation of stochastic nonconvex-strongly-concave optimization to gain finite-sample analysis, which would require simultaneously preserving the privacy on primal and dual sides. To this end, we employ a momentum-based stochastic gradient descent ascent to achieve a single-timescale algorithm, and achieve a good trade-off between meaningful privacy and utility guarantees of both the primal and dual sides by perturbing the gradients on both sides using well-calibrated Gaussian noises. As a result, our DPTD algorithm could provide $(\epsilon,\delta)$-differential privacy (DP) guarantee for the sensitive information encoded in transitions and retain the original power of TD learning, with the utility upper bounded by $\widetilde{\mathcal{O}}(\frac{(d\log(1/\delta))^{1/8}}{(n\epsilon)^{1/4}})$ (The tilde in this paper hides the log factor.), where $n$ is the trajectory length and $d$ is the dimension. Extensive experiments conducted in OpenAI Gym show the advantages of our proposed algorithm.

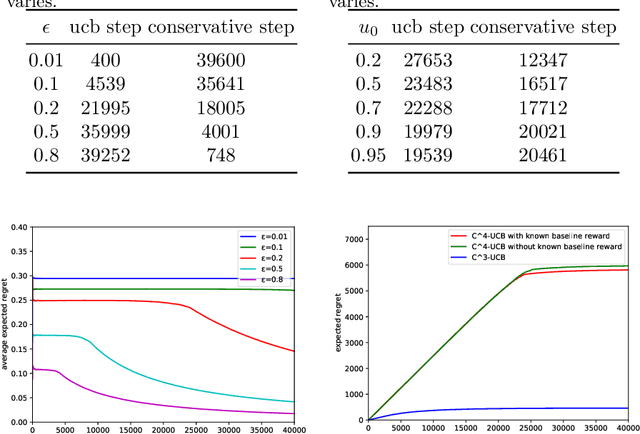
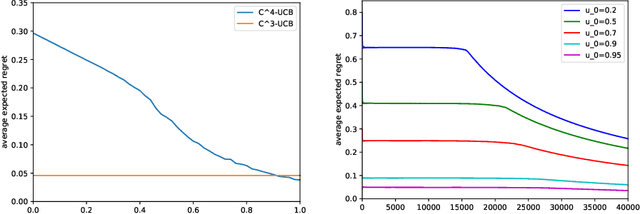
Conservative Contextual Combinatorial Cascading Bandit

Conservative mechanism is a desirable property in decision-making problems which balance the tradeoff between the exploration and exploitation. We propose the novel \emph{conservative contextual combinatorial cascading bandit ($C^4$-bandit)}, a cascading online learning game which incorporates the conservative mechanism. At each time step, the learning agent is given some contexts and has to recommend a list of items but not worse than the base strategy and then observes the reward by some stopping rules. We design the $C^4$-UCB algorithm to solve the problem and prove its n-step upper regret bound for two situations: known baseline reward and unknown baseline reward. The regret in both situations can be decomposed into two terms: (a) the upper bound for the general contextual combinatorial cascading bandit; and (b) a constant term for the regret from the conservative mechanism. We also improve the bound of the conservative contextual combinatorial bandit as a by-product. Experiments on synthetic data demonstrate its advantages and validate our theoretical analysis.