Differentially Private Temporal Difference Learning with Stochastic Nonconvex-Strongly-Concave Optimization
Paper and Code
Jan 25, 2022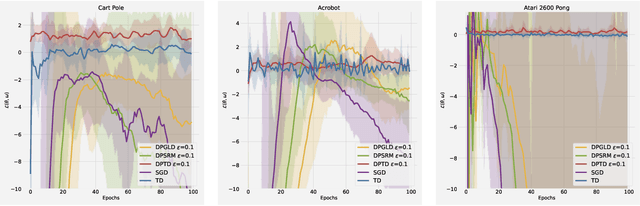
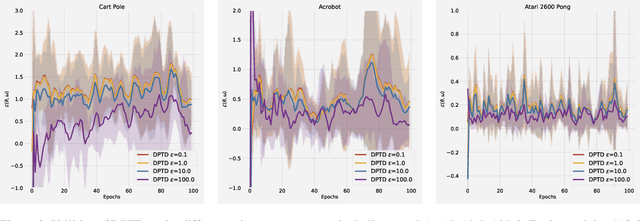
Temporal difference (TD) learning is a widely used method to evaluate policies in reinforcement learning. While many TD learning methods have been developed in recent years, little attention has been paid to preserving privacy and most of the existing approaches might face the concerns of data privacy from users. To enable complex representative abilities of policies, in this paper, we consider preserving privacy in TD learning with nonlinear value function approximation. This is challenging because such a nonlinear problem is usually studied in the formulation of stochastic nonconvex-strongly-concave optimization to gain finite-sample analysis, which would require simultaneously preserving the privacy on primal and dual sides. To this end, we employ a momentum-based stochastic gradient descent ascent to achieve a single-timescale algorithm, and achieve a good trade-off between meaningful privacy and utility guarantees of both the primal and dual sides by perturbing the gradients on both sides using well-calibrated Gaussian noises. As a result, our DPTD algorithm could provide $(\epsilon,\delta)$-differential privacy (DP) guarantee for the sensitive information encoded in transitions and retain the original power of TD learning, with the utility upper bounded by $\widetilde{\mathcal{O}}(\frac{(d\log(1/\delta))^{1/8}}{(n\epsilon)^{1/4}})$ (The tilde in this paper hides the log factor.), where $n$ is the trajectory length and $d$ is the dimension. Extensive experiments conducted in OpenAI Gym show the advantages of our proposed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge