Elucidating Rectified Flow with Deterministic Sampler: Polynomial Discretization Complexity for Multi and One-step Models

Recently, rectified flow (RF)-based models have achieved state-of-the-art performance in many areas for both the multi-step and one-step generation. However, only a few theoretical works analyze the discretization complexity of RF-based models. Existing works either focus on flow-based models with stochastic samplers or establish complexity results that exhibit exponential dependence on problem parameters. In this work, under the realistic bounded support assumption, we prove the first polynomial discretization complexity for multi-step and one-step RF-based models with a deterministic sampler simultaneously. For the multi-step setting, inspired by the predictor-corrector framework of diffusion models, we introduce a Langevin process as a corrector and show that RF-based models can achieve better polynomial discretization complexity than diffusion models. To achieve this result, we conduct a detailed analysis of the RF-based model and explain why it is better than previous popular models, such as variance preserving (VP) and variance exploding (VE)-based models. Based on the observation of multi-step RF-based models, we further provide the first polynomial discretization complexity result for one-step RF-based models, improving upon prior results for one-step diffusion-based models. These findings mark the first step toward theoretically understanding the impressive empirical performance of RF-based models in both multi-step and one-step generation.

Understanding Representation Learnability of Nonlinear Self-Supervised Learning

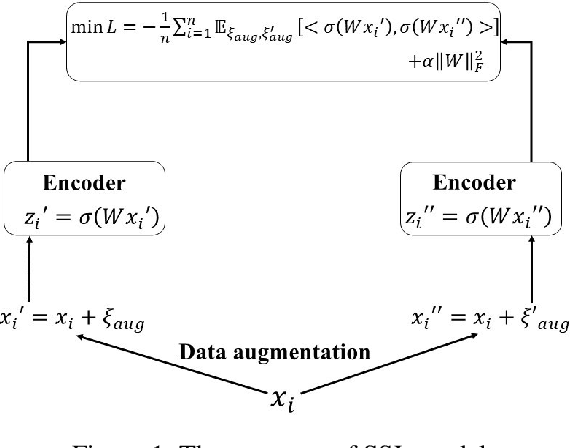
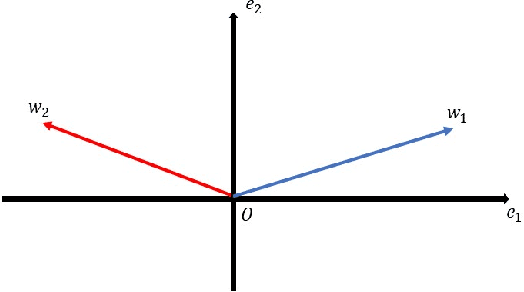
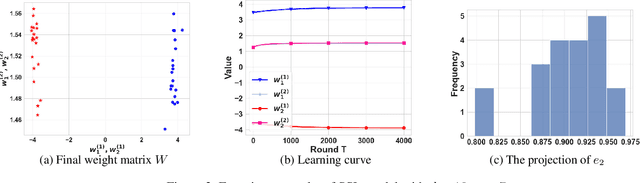
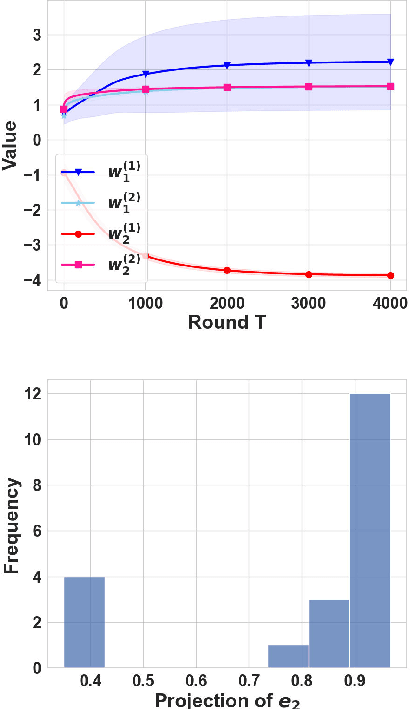
Self-supervised learning (SSL) has empirically shown its data representation learnability in many downstream tasks. There are only a few theoretical works on data representation learnability, and many of those focus on final data representation, treating the nonlinear neural network as a ``black box". However, the accurate learning results of neural networks are crucial for describing the data distribution features learned by SSL models. Our paper is the first to analyze the learning results of the nonlinear SSL model accurately. We consider a toy data distribution that contains two features: the label-related feature and the hidden feature. Unlike previous linear setting work that depends on closed-form solutions, we use the gradient descent algorithm to train a 1-layer nonlinear SSL model with a certain initialization region and prove that the model converges to a local minimum. Furthermore, different from the complex iterative analysis, we propose a new analysis process which uses the exact version of Inverse Function Theorem to accurately describe the features learned by the local minimum. With this local minimum, we prove that the nonlinear SSL model can capture the label-related feature and hidden feature at the same time. In contrast, the nonlinear supervised learning (SL) model can only learn the label-related feature. We also present the learning processes and results of the nonlinear SSL and SL model via simulation experiments.

Learning Adversarial Low-rank Markov Decision Processes with Unknown Transition and Full-information Feedback

In this work, we study the low-rank MDPs with adversarially changed losses in the full-information feedback setting. In particular, the unknown transition probability kernel admits a low-rank matrix decomposition \citep{REPUCB22}, and the loss functions may change adversarially but are revealed to the learner at the end of each episode. We propose a policy optimization-based algorithm POLO, and we prove that it attains the $\widetilde{O}(K^{\frac{5}{6}}A^{\frac{1}{2}}d\ln(1+M)/(1-\gamma)^2)$ regret guarantee, where $d$ is rank of the transition kernel (and hence the dimension of the unknown representations), $A$ is the cardinality of the action space, $M$ is the cardinality of the model class, and $\gamma$ is the discounted factor. Notably, our algorithm is oracle-efficient and has a regret guarantee with no dependence on the size of potentially arbitrarily large state space. Furthermore, we also prove an $\Omega(\frac{\gamma^2}{1-\gamma} \sqrt{d A K})$ regret lower bound for this problem, showing that low-rank MDPs are statistically more difficult to learn than linear MDPs in the regret minimization setting. To the best of our knowledge, we present the first algorithm that interleaves representation learning, exploration, and exploitation to achieve the sublinear regret guarantee for RL with nonlinear function approximation and adversarial losses.