Understanding Representation Learnability of Nonlinear Self-Supervised Learning
Paper and Code
Jan 06, 2024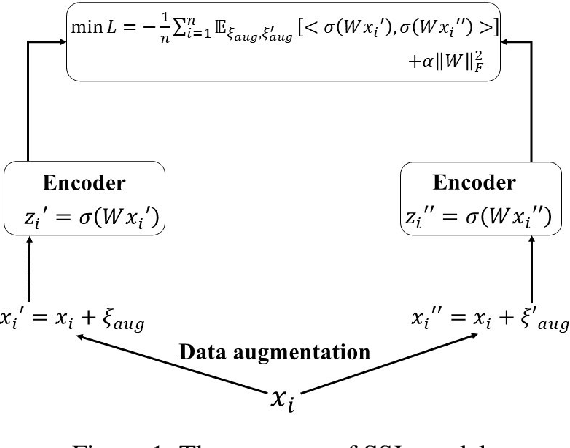
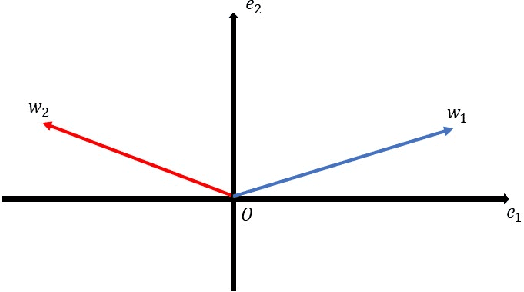
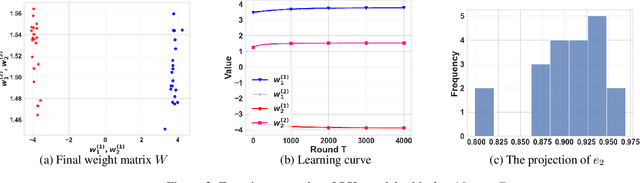
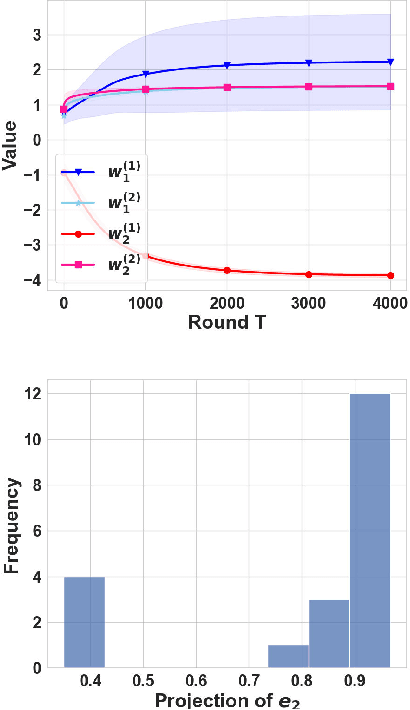
Self-supervised learning (SSL) has empirically shown its data representation learnability in many downstream tasks. There are only a few theoretical works on data representation learnability, and many of those focus on final data representation, treating the nonlinear neural network as a ``black box". However, the accurate learning results of neural networks are crucial for describing the data distribution features learned by SSL models. Our paper is the first to analyze the learning results of the nonlinear SSL model accurately. We consider a toy data distribution that contains two features: the label-related feature and the hidden feature. Unlike previous linear setting work that depends on closed-form solutions, we use the gradient descent algorithm to train a 1-layer nonlinear SSL model with a certain initialization region and prove that the model converges to a local minimum. Furthermore, different from the complex iterative analysis, we propose a new analysis process which uses the exact version of Inverse Function Theorem to accurately describe the features learned by the local minimum. With this local minimum, we prove that the nonlinear SSL model can capture the label-related feature and hidden feature at the same time. In contrast, the nonlinear supervised learning (SL) model can only learn the label-related feature. We also present the learning processes and results of the nonlinear SSL and SL model via simulation experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge