Visual Generation Unlocks Human-Like Reasoning through Multimodal World Models

Humans construct internal world models and reason by manipulating the concepts within these models. Recent advances in AI, particularly chain-of-thought (CoT) reasoning, approximate such human cognitive abilities, where world models are believed to be embedded within large language models. Expert-level performance in formal and abstract domains such as mathematics and programming has been achieved in current systems by relying predominantly on verbal reasoning. However, they still lag far behind humans in domains like physical and spatial intelligence, which require richer representations and prior knowledge. The emergence of unified multimodal models (UMMs) capable of both verbal and visual generation has therefore sparked interest in more human-like reasoning grounded in complementary multimodal pathways, though their benefits remain unclear. From a world-model perspective, this paper presents the first principled study of when and how visual generation benefits reasoning. Our key position is the visual superiority hypothesis: for certain tasks--particularly those grounded in the physical world--visual generation more naturally serves as world models, whereas purely verbal world models encounter bottlenecks arising from representational limitations or insufficient prior knowledge. Theoretically, we formalize internal world modeling as a core component of CoT reasoning and analyze distinctions among different forms of world models. Empirically, we identify tasks that necessitate interleaved visual-verbal CoT reasoning, constructing a new evaluation suite, VisWorld-Eval. Controlled experiments on a state-of-the-art UMM show that interleaved CoT significantly outperforms purely verbal CoT on tasks that favor visual world modeling, but offers no clear advantage otherwise. Together, this work clarifies the potential of multimodal world modeling for more powerful, human-like multimodal AI.

Inference-time Scaling of Diffusion Models through Classical Search

Classical search algorithms have long underpinned modern artificial intelligence. In this work, we tackle the challenge of inference-time control in diffusion models -- adapting generated outputs to meet diverse test-time objectives -- using principles from classical search. We propose a general framework that orchestrates local and global search to efficiently navigate the generative space. It employs a theoretically grounded local search via annealed Langevin MCMC and performs compute-efficient global exploration using breadth-first and depth-first tree search. We evaluate our approach on a range of challenging domains, including planning, offline reinforcement learning, and image generation. Across all tasks, we observe significant gains in both performance and efficiency. These results show that classical search provides a principled and practical foundation for inference-time scaling in diffusion models. Project page at diffusion-inference-scaling.github.io.

Domain Guidance: A Simple Transfer Approach for a Pre-trained Diffusion Model

Recent advancements in diffusion models have revolutionized generative modeling. However, the impressive and vivid outputs they produce often come at the cost of significant model scaling and increased computational demands. Consequently, building personalized diffusion models based on off-the-shelf models has emerged as an appealing alternative. In this paper, we introduce a novel perspective on conditional generation for transferring a pre-trained model. From this viewpoint, we propose *Domain Guidance*, a straightforward transfer approach that leverages pre-trained knowledge to guide the sampling process toward the target domain. Domain Guidance shares a formulation similar to advanced classifier-free guidance, facilitating better domain alignment and higher-quality generations. We provide both empirical and theoretical analyses of the mechanisms behind Domain Guidance. Our experimental results demonstrate its substantial effectiveness across various transfer benchmarks, achieving over a 19.6% improvement in FID and a 23.4% improvement in FD$_\text{DINOv2}$ compared to standard fine-tuning. Notably, existing fine-tuned models can seamlessly integrate Domain Guidance to leverage these benefits, without additional training.

ID policy (with reassignment) is asymptotically optimal for heterogeneous weakly-coupled MDPs

Heterogeneity poses a fundamental challenge for many real-world large-scale decision-making problems but remains largely understudied. In this paper, we study the fully heterogeneous setting of a prominent class of such problems, known as weakly-coupled Markov decision processes (WCMDPs). Each WCMDP consists of $N$ arms (or subproblems), which have distinct model parameters in the fully heterogeneous setting, leading to the curse of dimensionality when $N$ is large. We show that, under mild assumptions, a natural adaptation of the ID policy, although originally proposed for a homogeneous special case of WCMDPs, in fact achieves an $O(1/\sqrt{N})$ optimality gap in long-run average reward per arm for fully heterogeneous WCMDPs as $N$ becomes large. This is the first asymptotic optimality result for fully heterogeneous average-reward WCMDPs. Our techniques highlight the construction of a novel projection-based Lyapunov function, which witnesses the convergence of rewards and costs to an optimal region in the presence of heterogeneity.

Provable Risk-Sensitive Distributional Reinforcement Learning with General Function Approximation

In the realm of reinforcement learning (RL), accounting for risk is crucial for making decisions under uncertainty, particularly in applications where safety and reliability are paramount. In this paper, we introduce a general framework on Risk-Sensitive Distributional Reinforcement Learning (RS-DisRL), with static Lipschitz Risk Measures (LRM) and general function approximation. Our framework covers a broad class of risk-sensitive RL, and facilitates analysis of the impact of estimation functions on the effectiveness of RSRL strategies and evaluation of their sample complexity. We design two innovative meta-algorithms: \texttt{RS-DisRL-M}, a model-based strategy for model-based function approximation, and \texttt{RS-DisRL-V}, a model-free approach for general value function approximation. With our novel estimation techniques via Least Squares Regression (LSR) and Maximum Likelihood Estimation (MLE) in distributional RL with augmented Markov Decision Process (MDP), we derive the first $\widetilde{\mathcal{O}}(\sqrt{K})$ dependency of the regret upper bound for RSRL with static LRM, marking a pioneering contribution towards statistically efficient algorithms in this domain.

Improved Regret Bounds for Linear Adversarial MDPs via Linear Optimization

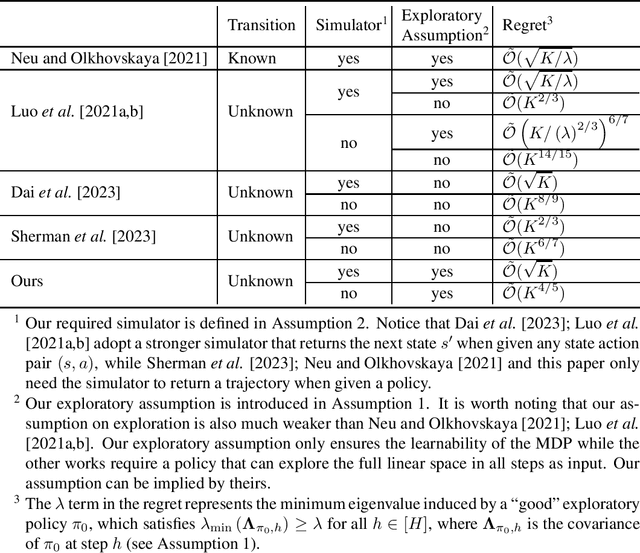
Learning Markov decision processes (MDP) in an adversarial environment has been a challenging problem. The problem becomes even more challenging with function approximation, since the underlying structure of the loss function and transition kernel are especially hard to estimate in a varying environment. In fact, the state-of-the-art results for linear adversarial MDP achieve a regret of $\tilde{O}(K^{6/7})$ ($K$ denotes the number of episodes), which admits a large room for improvement. In this paper, we investigate the problem with a new view, which reduces linear MDP into linear optimization by subtly setting the feature maps of the bandit arms of linear optimization. This new technique, under an exploratory assumption, yields an improved bound of $\tilde{O}(K^{4/5})$ for linear adversarial MDP without access to a transition simulator. The new view could be of independent interest for solving other MDP problems that possess a linear structure.