ID policy (with reassignment) is asymptotically optimal for heterogeneous weakly-coupled MDPs

Heterogeneity poses a fundamental challenge for many real-world large-scale decision-making problems but remains largely understudied. In this paper, we study the fully heterogeneous setting of a prominent class of such problems, known as weakly-coupled Markov decision processes (WCMDPs). Each WCMDP consists of $N$ arms (or subproblems), which have distinct model parameters in the fully heterogeneous setting, leading to the curse of dimensionality when $N$ is large. We show that, under mild assumptions, a natural adaptation of the ID policy, although originally proposed for a homogeneous special case of WCMDPs, in fact achieves an $O(1/\sqrt{N})$ optimality gap in long-run average reward per arm for fully heterogeneous WCMDPs as $N$ becomes large. This is the first asymptotic optimality result for fully heterogeneous average-reward WCMDPs. Our techniques highlight the construction of a novel projection-based Lyapunov function, which witnesses the convergence of rewards and costs to an optimal region in the presence of heterogeneity.

When is exponential asymptotic optimality achievable in average-reward restless bandits?

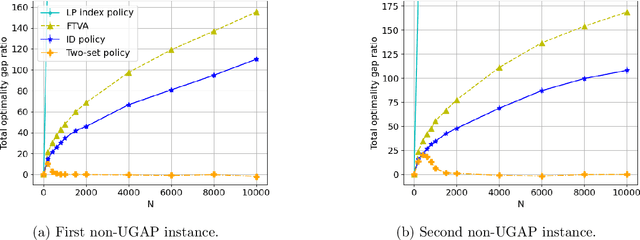
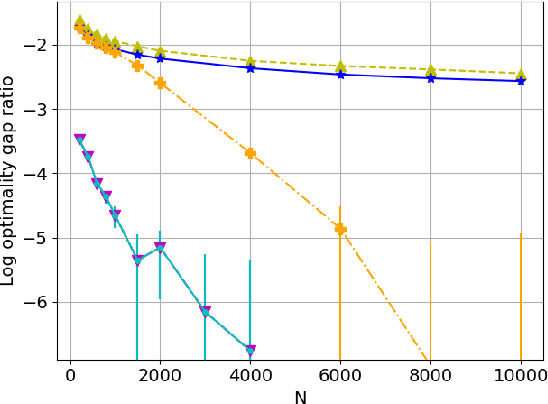
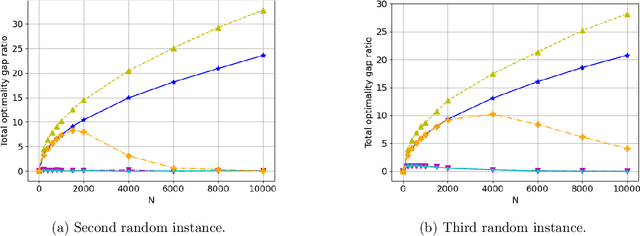
We consider the discrete-time infinite-horizon average-reward restless bandit problem. We propose a novel policy that maintains two dynamic subsets of arms: one subset of arms has a nearly optimal state distribution and takes actions according to an Optimal Local Control routine; the other subset of arms is driven towards the optimal state distribution and gradually merged into the first subset. We show that our policy is asymptotically optimal with an $O(\exp(-C N))$ optimality gap for an $N$-armed problem, under the mild assumptions of aperiodic-unichain, non-degeneracy, and local stability. Our policy is the first to achieve exponential asymptotic optimality under the above set of easy-to-verify assumptions, whereas prior work either requires a strong Global Attractor assumption or only achieves an $O(1/\sqrt{N})$ optimality gap. We further discuss the fundamental obstacles in significantly weakening our assumptions. In particular, we prove a lower bound showing that local stability is fundamental for exponential asymptotic optimality.

Unichain and Aperiodicity are Sufficient for Asymptotic Optimality of Average-Reward Restless Bandits

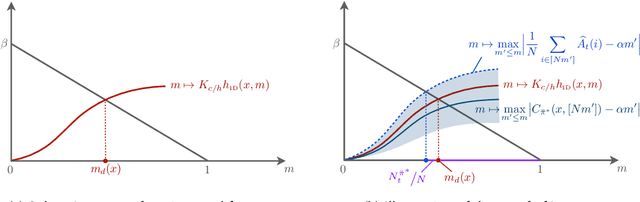
We consider the infinite-horizon, average-reward restless bandit problem in discrete time. We propose a new class of policies that are designed to drive a progressively larger subset of arms toward the optimal distribution. We show that our policies are asymptotically optimal with an $O(1/\sqrt{N})$ optimality gap for an $N$-armed problem, provided that the single-armed relaxed problem is unichain and aperiodic. Our approach departs from most existing work that focuses on index or priority policies, which rely on the Uniform Global Attractor Property (UGAP) to guarantee convergence to the optimum, or a recently developed simulation-based policy, which requires a Synchronization Assumption (SA).

Restless Bandits with Average Reward: Breaking the Uniform Global Attractor Assumption

We study the infinite-horizon restless bandit problem with the average reward criterion, under both discrete-time and continuous-time settings. A fundamental question is how to design computationally efficient policies that achieve a diminishing optimality gap as the number of arms, $N$, grows large. Existing results on asymptotical optimality all rely on the uniform global attractor property (UGAP), a complex and challenging-to-verify assumption. In this paper, we propose a general, simulation-based framework that converts any single-armed policy into a policy for the original $N$-armed problem. This is accomplished by simulating the single-armed policy on each arm and carefully steering the real state towards the simulated state. Our framework can be instantiated to produce a policy with an $O(1/\sqrt{N})$ optimality gap. In the discrete-time setting, our result holds under a simpler synchronization assumption, which covers some problem instances that do not satisfy UGAP. More notably, in the continuous-time setting, our result does not require any additional assumptions beyond the standard unichain condition. In both settings, we establish the first asymptotic optimality result that does not require UGAP.