When is exponential asymptotic optimality achievable in average-reward restless bandits?
Paper and Code
May 28, 2024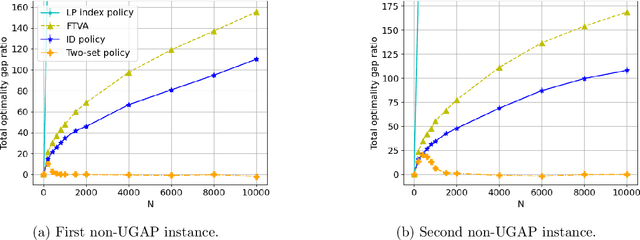
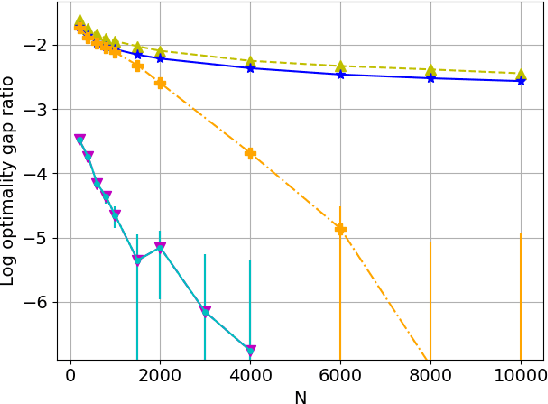
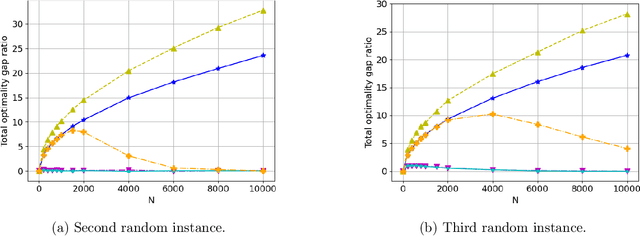
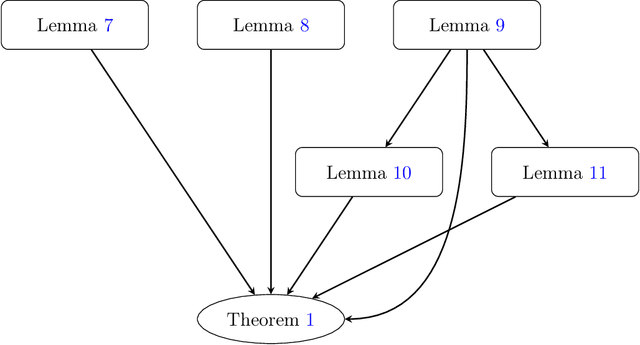
We consider the discrete-time infinite-horizon average-reward restless bandit problem. We propose a novel policy that maintains two dynamic subsets of arms: one subset of arms has a nearly optimal state distribution and takes actions according to an Optimal Local Control routine; the other subset of arms is driven towards the optimal state distribution and gradually merged into the first subset. We show that our policy is asymptotically optimal with an $O(\exp(-C N))$ optimality gap for an $N$-armed problem, under the mild assumptions of aperiodic-unichain, non-degeneracy, and local stability. Our policy is the first to achieve exponential asymptotic optimality under the above set of easy-to-verify assumptions, whereas prior work either requires a strong Global Attractor assumption or only achieves an $O(1/\sqrt{N})$ optimality gap. We further discuss the fundamental obstacles in significantly weakening our assumptions. In particular, we prove a lower bound showing that local stability is fundamental for exponential asymptotic optimality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge