Bioinspired Soft Spiral Robots for Versatile Grasping and Manipulation

Across various species and different scales, certain organisms use their appendages to grasp objects not through clamping but through wrapping. This pattern of movement is found in octopus tentacles, elephant trunks, and chameleon prehensile tails, demonstrating a great versatility to grasp a wide range of objects of various sizes and weights as well as dynamically manipulate them in the 3D space. We observed that the structures of these appendages follow a common pattern - a logarithmic spiral - which is especially challenging for existing robot designs to reproduce. This paper reports the design, fabrication, and operation of a class of cable-driven soft robots that morphologically replicate spiral-shaped wrapping. This amounts to substantially curling in length while actively controlling the curling direction as enabled by two principles: a) the parametric design based on the logarithmic spiral makes it possible to tightly pack to grasp objects that vary in size by more than two orders of magnitude and up to 260 times self-weight and b) asymmetric cable forces allow the swift control of the curling direction for conducting object manipulation. We demonstrate the ability to dynamically operate objects at a sub-second level by exploiting passive compliance. We believe that our study constitutes a step towards engineered systems that wrap to grasp and manipulate, and further sheds some insights into understanding the efficacy of biological spiral-shaped appendages.

FedADMM: A Robust Federated Deep Learning Framework with Adaptivity to System Heterogeneity

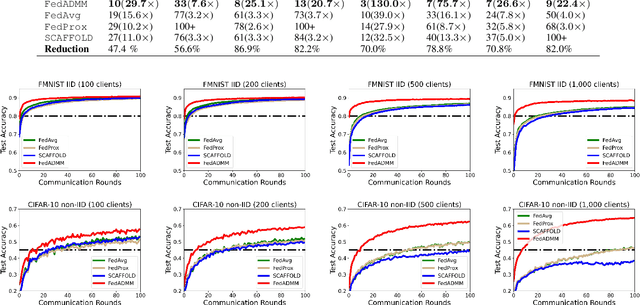
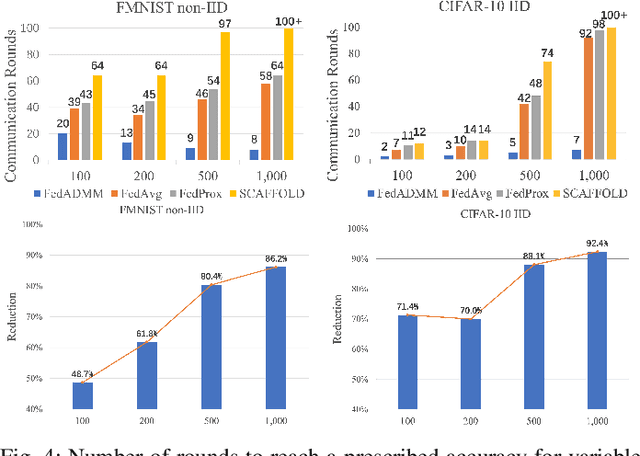
Federated Learning (FL) is an emerging framework for distributed processing of large data volumes by edge devices subject to limited communication bandwidths, heterogeneity in data distributions and computational resources, as well as privacy considerations. In this paper, we introduce a new FL protocol termed FedADMM based on primal-dual optimization. The proposed method leverages dual variables to tackle statistical heterogeneity, and accommodates system heterogeneity by tolerating variable amount of work performed by clients. FedADMM maintains identical communication costs per round as FedAvg/Prox, and generalizes them via the augmented Lagrangian. A convergence proof is established for nonconvex objectives, under no restrictions in terms of data dissimilarity or number of participants per round of the algorithm. We demonstrate the merits through extensive experiments on real datasets, under both IID and non-IID data distributions across clients. FedADMM consistently outperforms all baseline methods in terms of communication efficiency, with the number of rounds needed to reach a prescribed accuracy reduced by up to 87%. The algorithm effectively adapts to heterogeneous data distributions through the use of dual variables, without the need for hyperparameter tuning, and its advantages are more pronounced in large-scale systems.

Dynamical Modeling and Control of Soft Robots with Non-constant Curvature Deformation

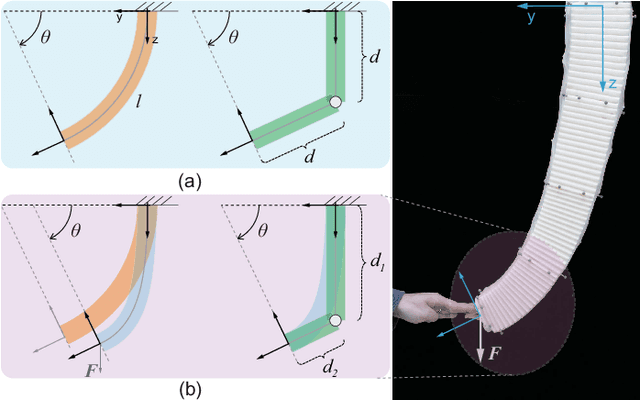
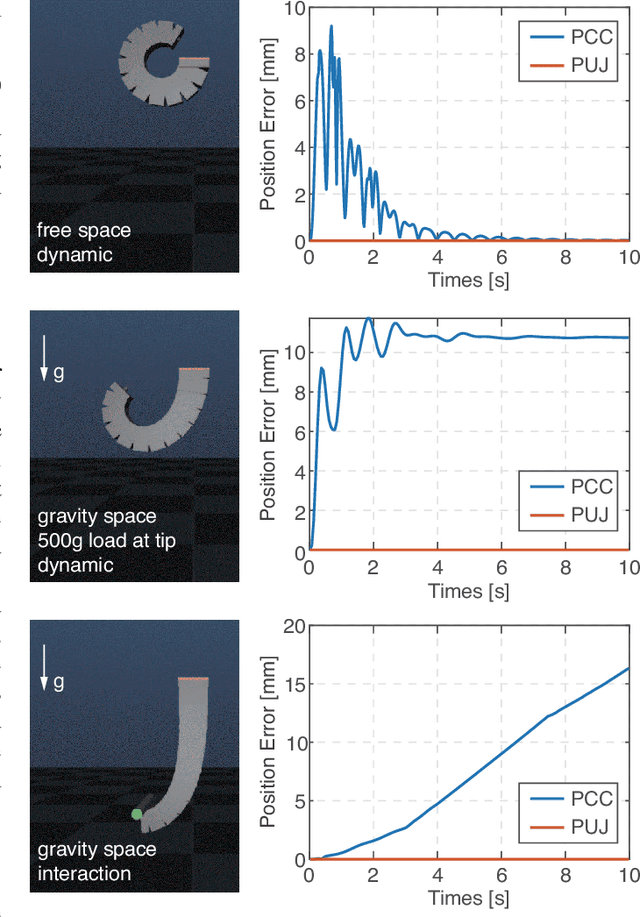
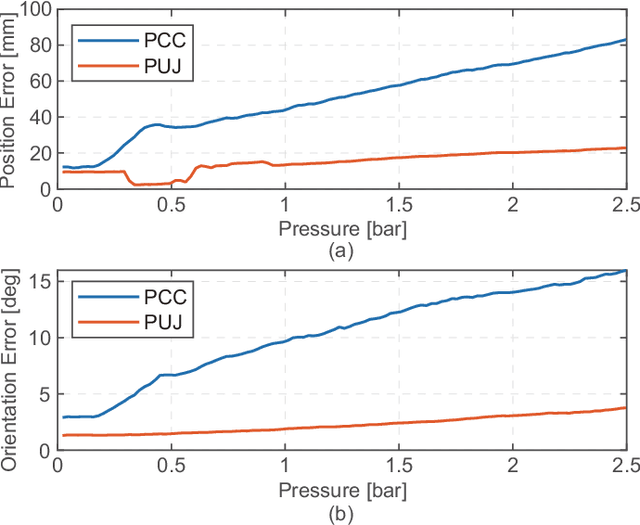
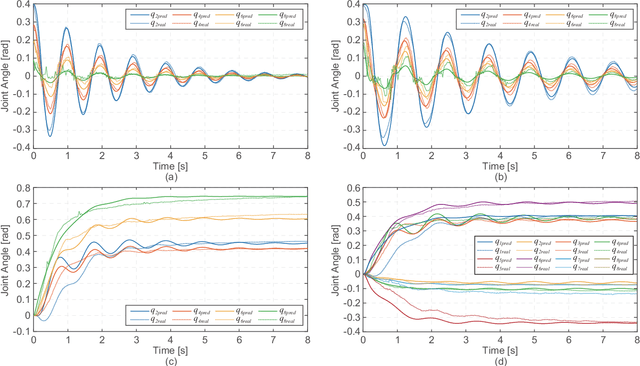
The Piecewise Constant Curvature (PCC) model is the most widely used soft robotic modeling and control. However, the PCC fails to accurately describe the deformation of the soft robots when executing dynamic tasks or interacting with the environment. This paper presents a simple threedimensional (3D) modeling method for a multi-segment soft robotic manipulator with non-constant curvature deformation. We devise kinematic and dynamical models for soft manipulators by modeling each segment of the manipulator as two stretchable links connected by a universal joint. Based on that, we present two controllers for dynamic trajectory tracking in confguration space and pose control in task space, respectively. Model accuracy is demonstrated with simulations and experimental data. The controllers are implemented on a four-segment soft robotic manipulator and validated in dynamic motions and pose control with unknown loads. The experimental results show that the dynamic controller enables a stable reference trajectory tracking at speeds up to 7m/s.

Control of a Soft Robotic Arm Using a Piecewise Universal Joint Model

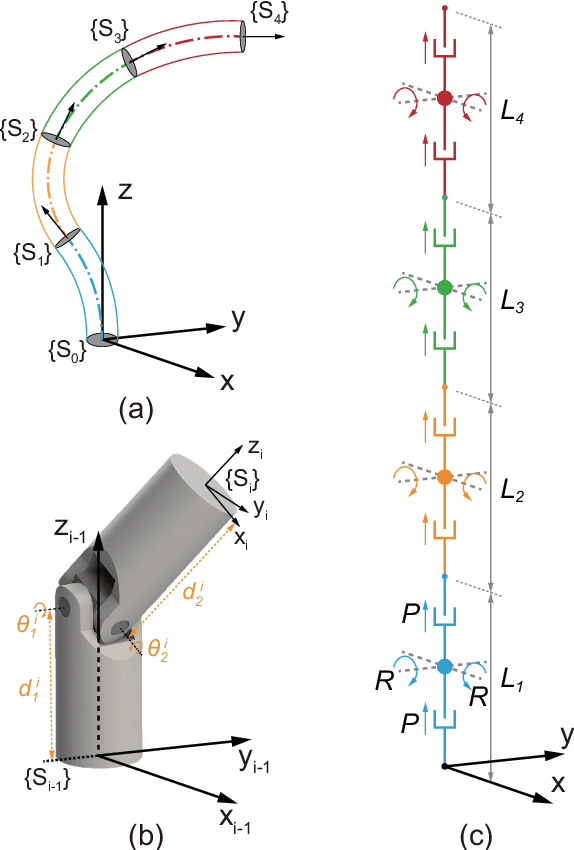
The 'infinite' passive degrees of freedom of soft robotic arms render their control especially challenging. In this paper, we leverage a previously developed model, which drawing equivalence of the soft arm to a series of universal joints, to design two closed-loop controllers: a configuration space controller for trajectory tracking and a task space controller for position control of the end effector. Extensive experiments and simulations on a four-segment soft arm attest to substantial improvement in terms of: a) superior tracking accuracy of the configuration space controller and b) reduced settling time and steady-state error of the task space controller. The task space controller is also verified to be effective in the presence of interactions between the soft arm and the environment.

A Novel Sequential Coreset Method for Gradient Descent Algorithms

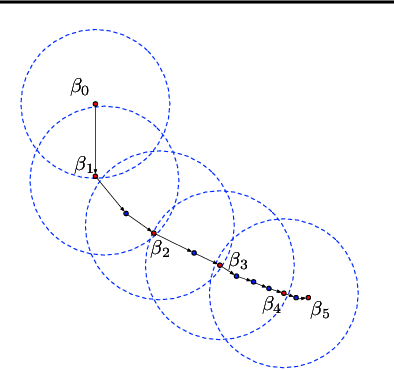
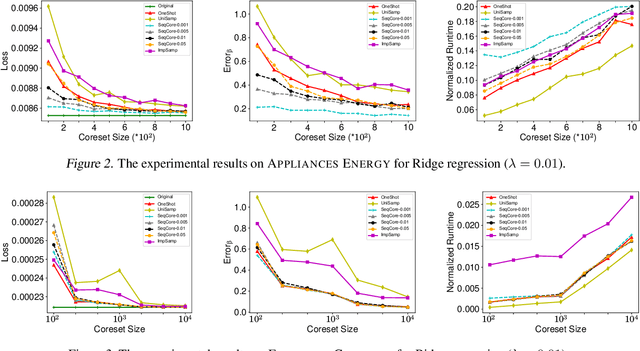
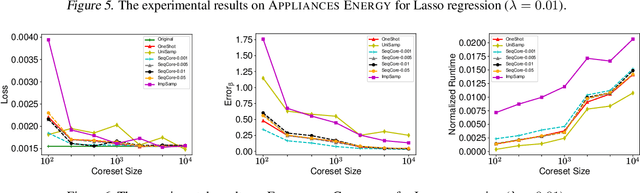
A wide range of optimization problems arising in machine learning can be solved by gradient descent algorithms, and a central question in this area is how to efficiently compress a large-scale dataset so as to reduce the computational complexity. {\em Coreset} is a popular data compression technique that has been extensively studied before. However, most of existing coreset methods are problem-dependent and cannot be used as a general tool for a broader range of applications. A key obstacle is that they often rely on the pseudo-dimension and total sensitivity bound that can be very high or hard to obtain. In this paper, based on the ''locality'' property of gradient descent algorithms, we propose a new framework, termed ''sequential coreset'', which effectively avoids these obstacles. Moreover, our method is particularly suitable for sparse optimization whence the coreset size can be further reduced to be only poly-logarithmically dependent on the dimension. In practice, the experimental results suggest that our method can save a large amount of running time compared with the baseline algorithms.

Unified Kinematic and Dynamical Modeling of a Soft Robotic Arm by a Piecewise Universal Joint Model

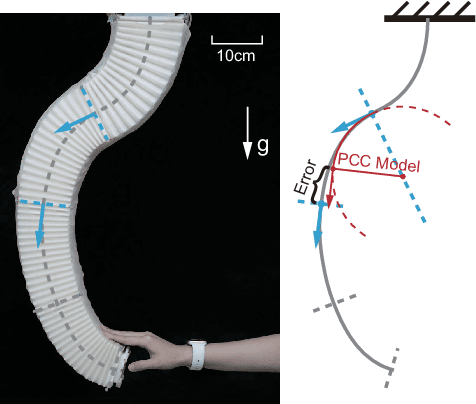
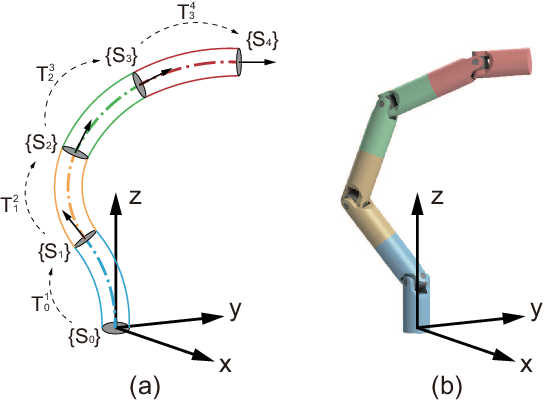
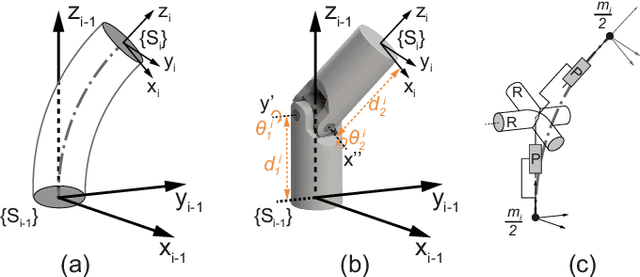
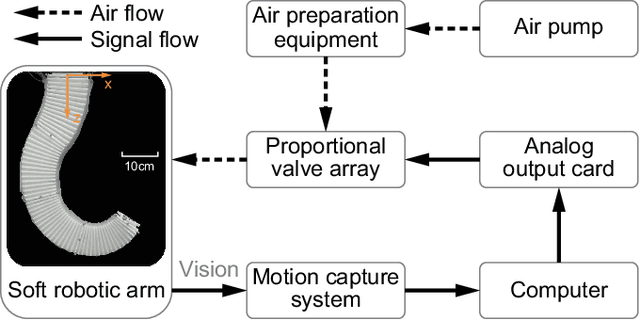
The compliance of soft robotic arms renders the development of accurate kinematic & dynamical models especially challenging. The most widely used model in soft robotic kinematics assumes Piecewise Constant Curvature (PCC). However, PCC fails to effectively handle external forces, or even the influence of gravity, since the robot does not deform with a constant curvature under these conditions. In this paper, we establish three-dimensional (3D) modeling of a multi-segment soft robotic arm under the less restrictive assumption that each segment of the arm is deformed on a plane without twisting. We devise a kinematic and dynamical model for the soft arm by deriving equivalence to a serial universal joint robot. Numerous experiments on the real robot platform along with simulations attest to the modeling accuracy of our approach in 3D motion with load. The maximum position/rotation error of the proposed model is verified 6.7x/4.6x lower than the PCC model considering gravity and external forces.

SUCAG: Stochastic Unbiased Curvature-aided Gradient Method for Distributed Optimization

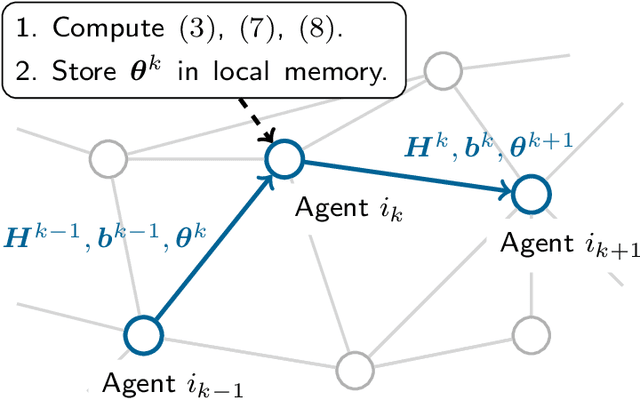
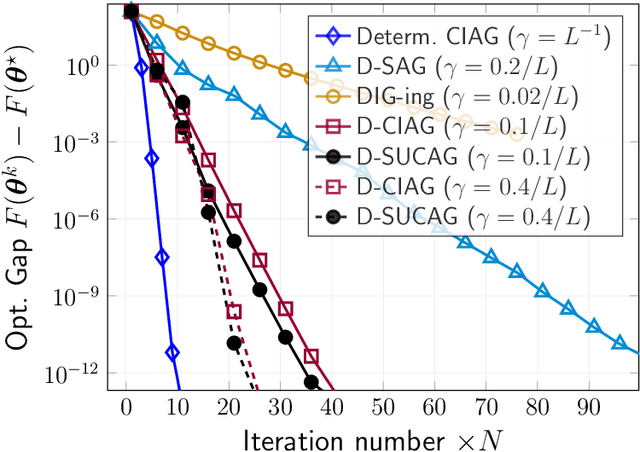
We propose and analyze a new stochastic gradient method, which we call Stochastic Unbiased Curvature-aided Gradient (SUCAG), for finite sum optimization problems. SUCAG constitutes an unbiased total gradient tracking technique that uses Hessian information to accelerate con- vergence. We analyze our method under the general asynchronous model of computation, in which each function is selected infinitely often with possibly unbounded (but sublinear) delay. For strongly convex problems, we establish linear convergence for the SUCAG method. When the initialization point is sufficiently close to the optimal solution, the established convergence rate is only dependent on the condition number of the problem, making it strictly faster than the known rate for the SAGA method. Furthermore, we describe a Markov-driven approach of implementing the SUCAG method in a distributed asynchronous multi-agent setting, via gossiping along a random walk on an undirected communication graph. We show that our analysis applies as long as the graph is connected and, notably, establishes an asymptotic linear convergence rate that is robust to the graph topology. Numerical results demonstrate the merits of our algorithm over existing methods.

Sparse Travel Time Estimation from Streaming Data

We address two shortcomings in online travel time estimation methods for congested urban traffic. The first shortcoming is related to the determination of the number of mixture modes, which can change dynamically, within day and from day to day. The second shortcoming is the wide-spread use of Gaussian probability densities as mixture components. Gaussian densities fail to capture the positive skew in travel time distributions and, consequently, large numbers of mixture components are needed for reasonable fitting accuracy when applied as mixture components. They also assign positive probabilities to negative travel times. To address these issues, this paper develops a mixture distribution with asymmetric components supported on the positive numbers. We use sparse estimation techniques to ensure parsimonious models. Specifically, we derive a novel generalization of Gamma mixture densities using Mittag-Leffler functions, which provides enhanced fitting flexibility and improved parsimony. In order to accommodate within-day variability and allow for online implementation of the proposed methodology (i.e., fast computations on streaming travel time data), we introduce a recursive algorithm which efficiently updates the fitted distribution whenever new data become available. Experimental results using real-world travel time data illustrate the efficacy of the proposed methods.

Recursive Compressed Sensing

We introduce a recursive algorithm for performing compressed sensing on streaming data. The approach consists of a) recursive encoding, where we sample the input stream via overlapping windowing and make use of the previous measurement in obtaining the next one, and b) recursive decoding, where the signal estimate from the previous window is utilized in order to achieve faster convergence in an iterative optimization scheme applied to decode the new one. To remove estimation bias, a two-step estimation procedure is proposed comprising support set detection and signal amplitude estimation. Estimation accuracy is enhanced by a non-linear voting method and averaging estimates over multiple windows. We analyze the computational complexity and estimation error, and show that the normalized error variance asymptotically goes to zero for sublinear sparsity. Our simulation results show speed up of an order of magnitude over traditional CS, while obtaining significantly lower reconstruction error under mild conditions on the signal magnitudes and the noise level.