FlowMixer: A Constrained Neural Architecture for Interpretable Spatiotemporal Forecasting

We introduce FlowMixer, a neural architecture that leverages constrained matrix operations to model structured spatiotemporal patterns. At its core, FlowMixer incorporates non-negative matrix mixing layers within a reversible mapping framework-applying transforms before mixing and their inverses afterward. This shape-preserving design enables a Kronecker-Koopman eigenmode framework that bridges statistical learning with dynamical systems theory, providing interpretable spatiotemporal patterns and facilitating direct algebraic manipulation of prediction horizons without retraining. Extensive experiments across diverse domains demonstrate FlowMixer's robust long-horizon forecasting capabilities while effectively modeling physical phenomena such as chaotic attractors and turbulent flows. These results suggest that architectural constraints can simultaneously enhance predictive performance and mathematical interpretability in neural forecasting systems.

Koopman Autoencoders Learn Neural Representation Dynamics

This paper explores a simple question: can we model the internal transformations of a neural network using dynamical systems theory? We introduce Koopman autoencoders to capture how neural representations evolve through network layers, treating these representations as states in a dynamical system. Our approach learns a surrogate model that predicts how neural representations transform from input to output, with two key advantages. First, by way of lifting the original states via an autoencoder, it operates in a linear space, making editing the dynamics straightforward. Second, it preserves the topologies of the original representations by regularizing the autoencoding objective. We demonstrate that these surrogate models naturally replicate the progressive topological simplification observed in neural networks. As a practical application, we show how our approach enables targeted class unlearning in the Yin-Yang and MNIST classification tasks.

Catastrophic Overfitting, Entropy Gap and Participation Ratio: A Noiseless $l^p$ Norm Solution for Fast Adversarial Training

Adversarial training is a cornerstone of robust deep learning, but fast methods like the Fast Gradient Sign Method (FGSM) often suffer from Catastrophic Overfitting (CO), where models become robust to single-step attacks but fail against multi-step variants. While existing solutions rely on noise injection, regularization, or gradient clipping, we propose a novel solution that purely controls the $l^p$ training norm to mitigate CO. Our study is motivated by the empirical observation that CO is more prevalent under the $l^{\infty}$ norm than the $l^2$ norm. Leveraging this insight, we develop a framework for generalized $l^p$ attack as a fixed point problem and craft $l^p$-FGSM attacks to understand the transition mechanics from $l^2$ to $l^{\infty}$. This leads to our core insight: CO emerges when highly concentrated gradients where information localizes in few dimensions interact with aggressive norm constraints. By quantifying gradient concentration through Participation Ratio and entropy measures, we develop an adaptive $l^p$-FGSM that automatically tunes the training norm based on gradient information. Extensive experiments demonstrate that this approach achieves strong robustness without requiring additional regularization or noise injection, providing a novel and theoretically-principled pathway to mitigate the CO problem.

Neural operators struggle to learn complex PDEs in pedestrian mobility: Hughes model case study

This paper investigates the limitations of neural operators in learning solutions for a Hughes model, a first-order hyperbolic conservation law system for crowd dynamics. The model couples a Fokker-Planck equation representing pedestrian density with a Hamilton-Jacobi-type (eikonal) equation. This Hughes model belongs to the class of nonlinear hyperbolic systems that often exhibit complex solution structures, including shocks and discontinuities. In this study, we assess the performance of three state-of-the-art neural operators (Fourier Neural Operator, Wavelet Neural Operator, and Multiwavelet Neural Operator) in various challenging scenarios. Specifically, we consider (1) discontinuous and Gaussian initial conditions and (2) diverse boundary conditions, while also examining the impact of different numerical schemes. Our results show that these neural operators perform well in easy scenarios with fewer discontinuities in the initial condition, yet they struggle in complex scenarios with multiple initial discontinuities and dynamic boundary conditions, even when trained specifically on such complex samples. The predicted solutions often appear smoother, resulting in a reduction in total variation and a loss of important physical features. This smoothing behavior is similar to issues discussed by Daganzo (1995), where models that introduce artificial diffusion were shown to miss essential features such as shock waves in hyperbolic systems. These results suggest that current neural operator architectures may introduce unintended regularization effects that limit their ability to capture transport dynamics governed by discontinuities. They also raise concerns about generalizing these methods to traffic applications where shock preservation is essential.

Urban traffic analysis and forecasting through shared Koopman eigenmodes

Predicting traffic flow in data-scarce cities is challenging due to limited historical data. To address this, we leverage transfer learning by identifying periodic patterns common to data-rich cities using a customized variant of Dynamic Mode Decomposition (DMD): constrained Hankelized DMD (TrHDMD). This method uncovers common eigenmodes (urban heartbeats) in traffic patterns and transfers them to data-scarce cities, significantly enhancing prediction performance. TrHDMD reduces the need for extensive training datasets by utilizing prior knowledge from other cities. By applying Koopman operator theory to multi-city loop detector data, we identify stable, interpretable, and time-invariant traffic modes. Injecting ``urban heartbeats'' into forecasting tasks improves prediction accuracy and has the potential to enhance traffic management strategies for cities with varying data infrastructures. Our work introduces cross-city knowledge transfer via shared Koopman eigenmodes, offering actionable insights and reliable forecasts for data-scarce urban environments.

Representing Neural Network Layers as Linear Operations via Koopman Operator Theory

The strong performance of simple neural networks is often attributed to their nonlinear activations. However, a linear view of neural networks makes understanding and controlling networks much more approachable. We draw from a dynamical systems view of neural networks, offering a fresh perspective by using Koopman operator theory and its connections with dynamic mode decomposition (DMD). Together, they offer a framework for linearizing dynamical systems by embedding the system into an appropriate observable space. By reframing a neural network as a dynamical system, we demonstrate that we can replace the nonlinear layer in a pretrained multi-layer perceptron (MLP) with a finite-dimensional linear operator. In addition, we analyze the eigenvalues of DMD and the right singular vectors of SVD, to present evidence that time-delayed coordinates provide a straightforward and highly effective observable space for Koopman theory to linearize a network layer. Consequently, we replace layers of an MLP trained on the Yin-Yang dataset with predictions from a DMD model, achieving a mdoel accuracy of up to 97.3%, compared to the original 98.4%. In addition, we replace layers in an MLP trained on the MNIST dataset, achieving up to 95.8%, compared to the original 97.2% on the test set.

Fourier neural operator for learning solutions to macroscopic traffic flow models: Application to the forward and inverse problems

Deep learning methods are emerging as popular computational tools for solving forward and inverse problems in traffic flow. In this paper, we study a neural operator framework for learning solutions to nonlinear hyperbolic partial differential equations with applications in macroscopic traffic flow models. In this framework, an operator is trained to map heterogeneous and sparse traffic input data to the complete macroscopic traffic state in a supervised learning setting. We chose a physics-informed Fourier neural operator ($\pi$-FNO) as the operator, where an additional physics loss based on a discrete conservation law regularizes the problem during training to improve the shock predictions. We also propose to use training data generated from random piecewise constant input data to systematically capture the shock and rarefied solutions. From experiments using the LWR traffic flow model, we found superior accuracy in predicting the density dynamics of a ring-road network and urban signalized road. We also found that the operator can be trained using simple traffic density dynamics, e.g., consisting of $2-3$ vehicle queues and $1-2$ traffic signal cycles, and it can predict density dynamics for heterogeneous vehicle queue distributions and multiple traffic signal cycles $(\geq 2)$ with an acceptable error. The extrapolation error grew sub-linearly with input complexity for a proper choice of the model architecture and training data. Adding a physics regularizer aided in learning long-term traffic density dynamics, especially for problems with periodic boundary data.

Physical Backdoor Trigger Activation of Autonomous Vehicle using Reachability Analysis

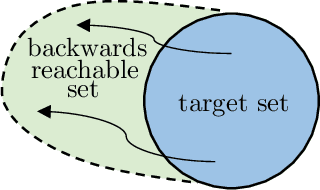
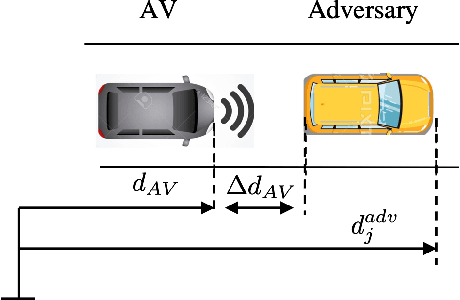
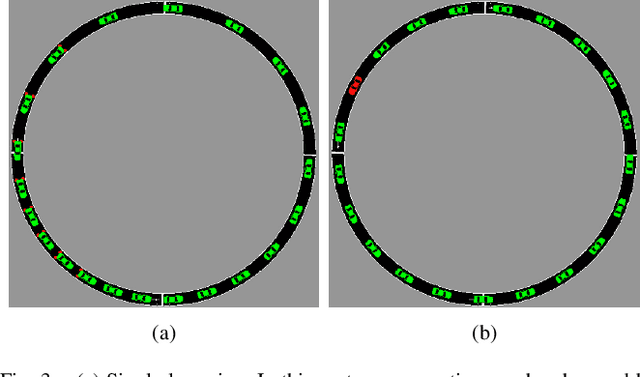
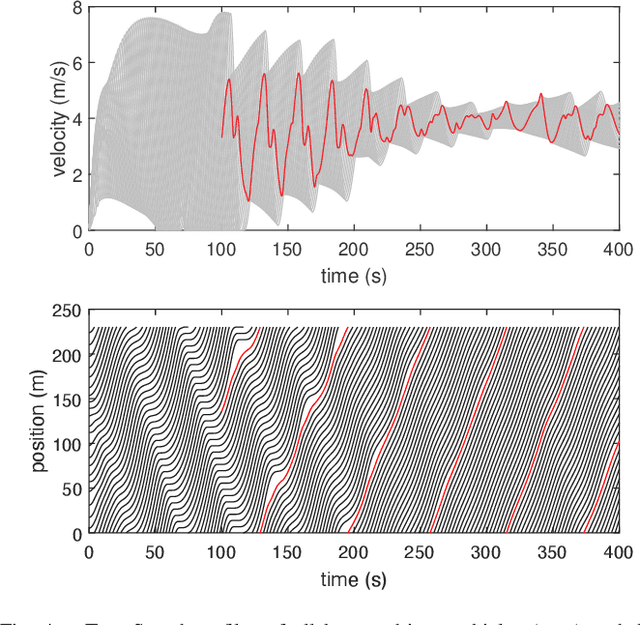
Recent studies reveal that Autonomous Vehicles (AVs) can be manipulated by hidden backdoors, causing them to perform harmful actions when activated by physical triggers. However, it is still unclear how these triggers can be activated while adhering to traffic principles. Understanding this vulnerability in a dynamic traffic environment is crucial. This work addresses this gap by presenting physical trigger activation as a reachability problem of controlled dynamic system. Our technique identifies security-critical areas in traffic systems where trigger conditions for accidents can be reached, and provides intended trajectories for how those conditions can be reached. Testing on typical traffic scenarios showed the system can be successfully driven to trigger conditions with near 100% activation rate. Our method benefits from identifying AV vulnerability and enabling effective safety strategies.

Optimal Smoothing Distribution Exploration for Backdoor Neutralization in Deep Learning-based Traffic Systems

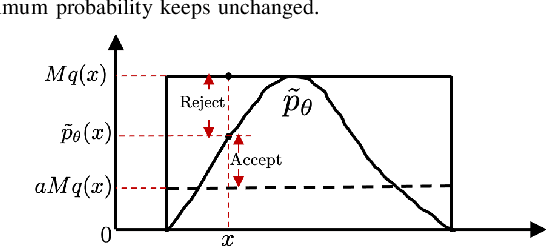
Deep Reinforcement Learning (DRL) enhances the efficiency of Autonomous Vehicles (AV), but also makes them susceptible to backdoor attacks that can result in traffic congestion or collisions. Backdoor functionality is typically incorporated by contaminating training datasets with covert malicious data to maintain high precision on genuine inputs while inducing the desired (malicious) outputs for specific inputs chosen by adversaries. Current defenses against backdoors mainly focus on image classification using image-based features, which cannot be readily transferred to the regression task of DRL-based AV controllers since the inputs are continuous sensor data, i.e., the combinations of velocity and distance of AV and its surrounding vehicles. Our proposed method adds well-designed noise to the input to neutralize backdoors. The approach involves learning an optimal smoothing (noise) distribution to preserve the normal functionality of genuine inputs while neutralizing backdoors. By doing so, the resulting model is expected to be more resilient against backdoor attacks while maintaining high accuracy on genuine inputs. The effectiveness of the proposed method is verified on a simulated traffic system based on a microscopic traffic simulator, where experimental results showcase that the smoothed traffic controller can neutralize all trigger samples and maintain the performance of relieving traffic congestion

Learning-based solutions to nonlinear hyperbolic PDEs: Empirical insights on generalization errors

We study learning weak solutions to nonlinear hyperbolic partial differential equations (H-PDE), which have been difficult to learn due to discontinuities in their solutions. We use a physics-informed variant of the Fourier Neural Operator ($\pi$-FNO) to learn the weak solutions. We empirically quantify the generalization/out-of-sample error of the $\pi$-FNO solver as a function of input complexity, i.e., the distributions of initial and boundary conditions. Our testing results show that $\pi$-FNO generalizes well to unseen initial and boundary conditions. We find that the generalization error grows linearly with input complexity. Further, adding a physics-informed regularizer improved the prediction of discontinuities in the solution. We use the Lighthill-Witham-Richards (LWR) traffic flow model as a guiding example to illustrate the results.