Representing Neural Network Layers as Linear Operations via Koopman Operator Theory

The strong performance of simple neural networks is often attributed to their nonlinear activations. However, a linear view of neural networks makes understanding and controlling networks much more approachable. We draw from a dynamical systems view of neural networks, offering a fresh perspective by using Koopman operator theory and its connections with dynamic mode decomposition (DMD). Together, they offer a framework for linearizing dynamical systems by embedding the system into an appropriate observable space. By reframing a neural network as a dynamical system, we demonstrate that we can replace the nonlinear layer in a pretrained multi-layer perceptron (MLP) with a finite-dimensional linear operator. In addition, we analyze the eigenvalues of DMD and the right singular vectors of SVD, to present evidence that time-delayed coordinates provide a straightforward and highly effective observable space for Koopman theory to linearize a network layer. Consequently, we replace layers of an MLP trained on the Yin-Yang dataset with predictions from a DMD model, achieving a mdoel accuracy of up to 97.3%, compared to the original 98.4%. In addition, we replace layers in an MLP trained on the MNIST dataset, achieving up to 95.8%, compared to the original 97.2% on the test set.

Exploring the Interplay of Interpretability and Robustness in Deep Neural Networks: A Saliency-guided Approach

Adversarial attacks pose a significant challenge to deploying deep learning models in safety-critical applications. Maintaining model robustness while ensuring interpretability is vital for fostering trust and comprehension in these models. This study investigates the impact of Saliency-guided Training (SGT) on model robustness, a technique aimed at improving the clarity of saliency maps to deepen understanding of the model's decision-making process. Experiments were conducted on standard benchmark datasets using various deep learning architectures trained with and without SGT. Findings demonstrate that SGT enhances both model robustness and interpretability. Additionally, we propose a novel approach combining SGT with standard adversarial training to achieve even greater robustness while preserving saliency map quality. Our strategy is grounded in the assumption that preserving salient features crucial for correctly classifying adversarial examples enhances model robustness, while masking non-relevant features improves interpretability. Our technique yields significant gains, achieving a 35\% and 20\% improvement in robustness against PGD attack with noise magnitudes of $0.2$ and $0.02$ for the MNIST and CIFAR-10 datasets, respectively, while producing high-quality saliency maps.

Examining Changes in Internal Representations of Continual Learning Models Through Tensor Decomposition

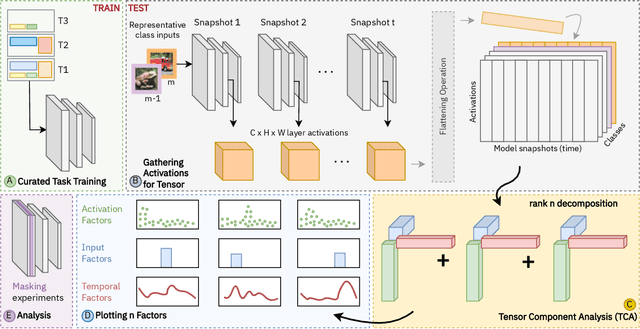
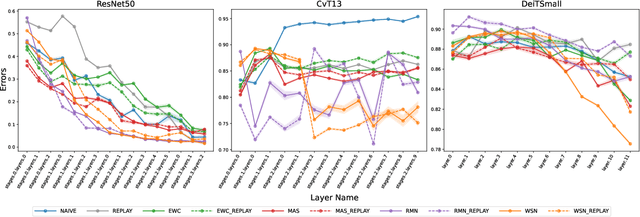
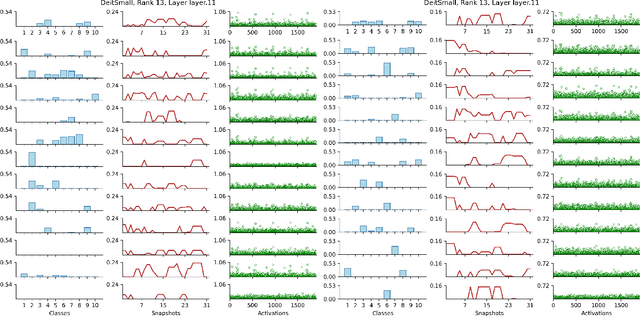
Continual learning (CL) has spurred the development of several methods aimed at consolidating previous knowledge across sequential learning. Yet, the evaluations of these methods have primarily focused on the final output, such as changes in the accuracy of predicted classes, overlooking the issue of representational forgetting within the model. In this paper, we propose a novel representation-based evaluation framework for CL models. This approach involves gathering internal representations from throughout the continual learning process and formulating three-dimensional tensors. The tensors are formed by stacking representations, such as layer activations, generated from several inputs and model `snapshots', throughout the learning process. By conducting tensor component analysis (TCA), we aim to uncover meaningful patterns about how the internal representations evolve, expecting to highlight the merits or shortcomings of examined CL strategies. We conduct our analyses across different model architectures and importance-based continual learning strategies, with a curated task selection. While the results of our approach mirror the difference in performance of various CL strategies, we found that our methodology did not directly highlight specialized clusters of neurons, nor provide an immediate understanding the evolution of filters. We believe a scaled down version of our approach will provide insight into the benefits and pitfalls of using TCA to study continual learning dynamics.