Urban traffic analysis and forecasting through shared Koopman eigenmodes

Predicting traffic flow in data-scarce cities is challenging due to limited historical data. To address this, we leverage transfer learning by identifying periodic patterns common to data-rich cities using a customized variant of Dynamic Mode Decomposition (DMD): constrained Hankelized DMD (TrHDMD). This method uncovers common eigenmodes (urban heartbeats) in traffic patterns and transfers them to data-scarce cities, significantly enhancing prediction performance. TrHDMD reduces the need for extensive training datasets by utilizing prior knowledge from other cities. By applying Koopman operator theory to multi-city loop detector data, we identify stable, interpretable, and time-invariant traffic modes. Injecting ``urban heartbeats'' into forecasting tasks improves prediction accuracy and has the potential to enhance traffic management strategies for cities with varying data infrastructures. Our work introduces cross-city knowledge transfer via shared Koopman eigenmodes, offering actionable insights and reliable forecasts for data-scarce urban environments.

Generalized adaptive smoothing based neural network architecture for traffic state estimation

The adaptive smoothing method (ASM) is a standard data-driven technique used in traffic state estimation. The ASM has free parameters which, in practice, are chosen to be some generally acceptable values based on intuition. However, we note that the heuristically chosen values often result in un-physical predictions by the ASM. In this work, we propose a neural network based on the ASM which tunes those parameters automatically by learning from sparse data from road sensors. We refer to it as the adaptive smoothing neural network (ASNN). We also propose a modified ASNN (MASNN), which makes it a strong learner by using ensemble averaging. The ASNN and MASNN are trained and tested two real-world datasets. Our experiments reveal that the ASNN and the MASNN outperform the conventional ASM.

Short-Term Traffic Forecasting Using High-Resolution Traffic Data

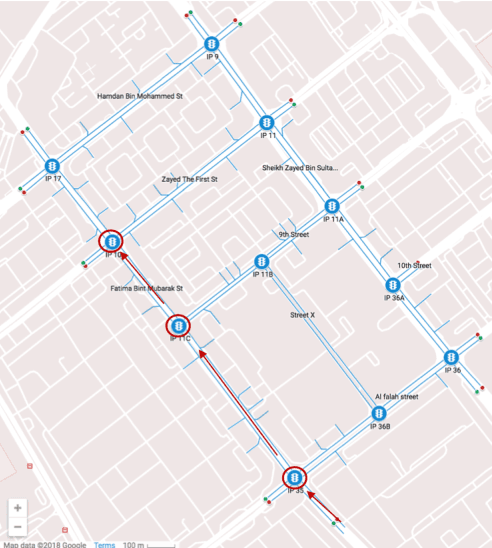
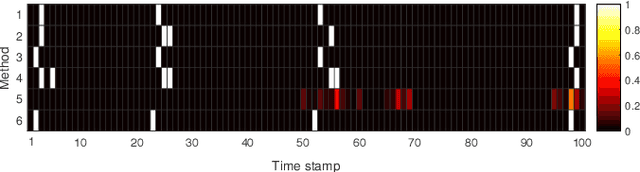
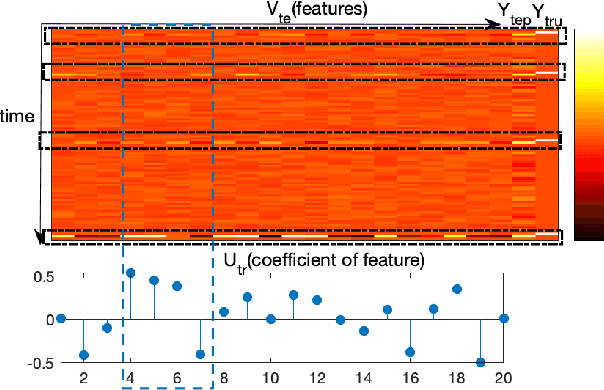
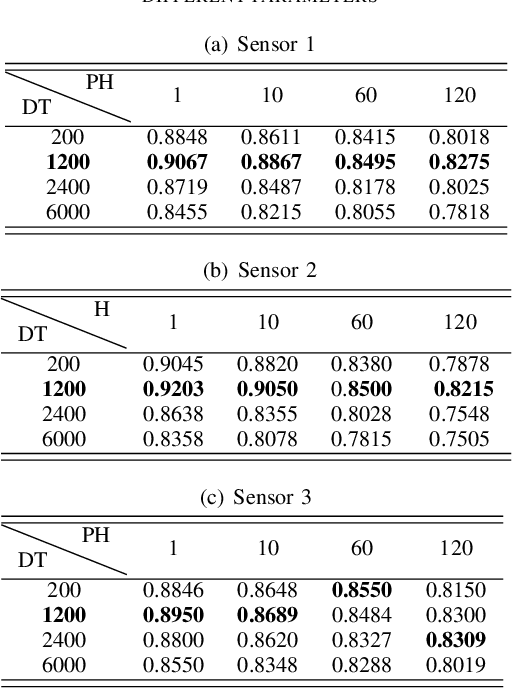
This paper develops a data-driven toolkit for traffic forecasting using high-resolution (a.k.a. event-based) traffic data. This is the raw data obtained from fixed sensors in urban roads. Time series of such raw data exhibit heavy fluctuations from one time step to the next (typically on the order of 0.1-1 second). Short-term forecasts (10-30 seconds into the future) of traffic conditions are critical for traffic operations applications (e.g., adaptive signal control). But traffic forecasting tools in the literature deal predominantly with 3-5 minute aggregated data, where the typical signal cycle is on the order of 2 minutes. This renders such forecasts useless at the operations level. To this end, we model the traffic forecasting problem as a matrix completion problem, where the forecasting inputs are mapped to a higher dimensional space using kernels. The formulation allows us to capture both nonlinear dependencies between forecasting inputs and outputs but also allows us to capture dependencies among the inputs. These dependencies correspond to correlations between different locations in the network. We further employ adaptive boosting to enhance the training accuracy and capture historical patterns in the data. The performance of the proposed methods is verified using high-resolution data obtained from a real-world traffic network in Abu Dhabi, UAE. Our experimental results show that the proposed method outperforms other state-of-the-art algorithms.

Nonlinear Traffic Prediction as a Matrix Completion Problem with Ensemble Learning

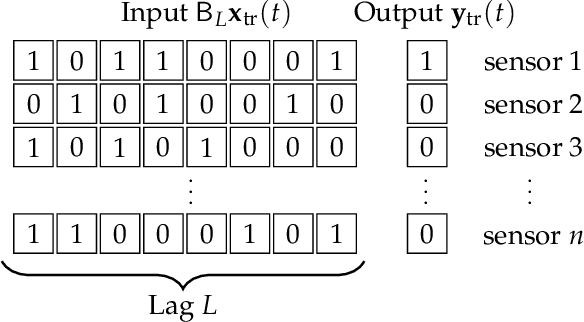
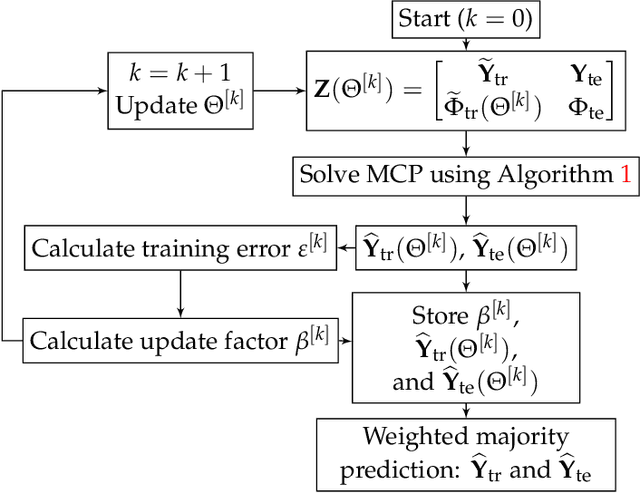
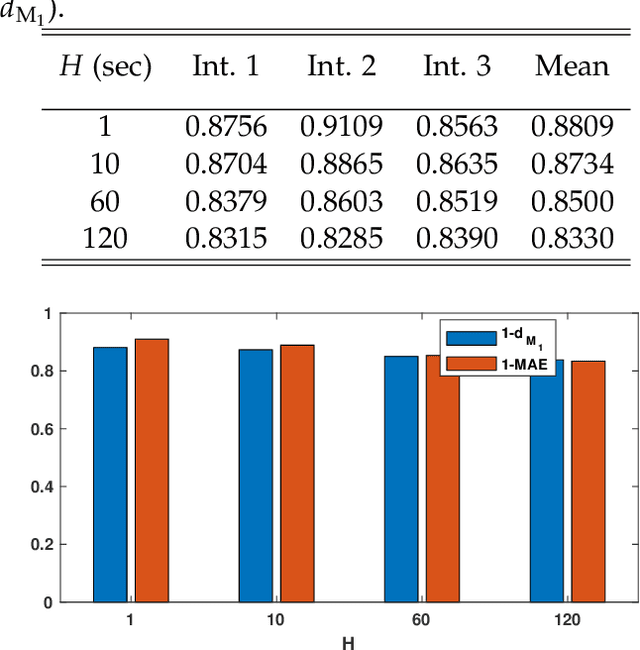
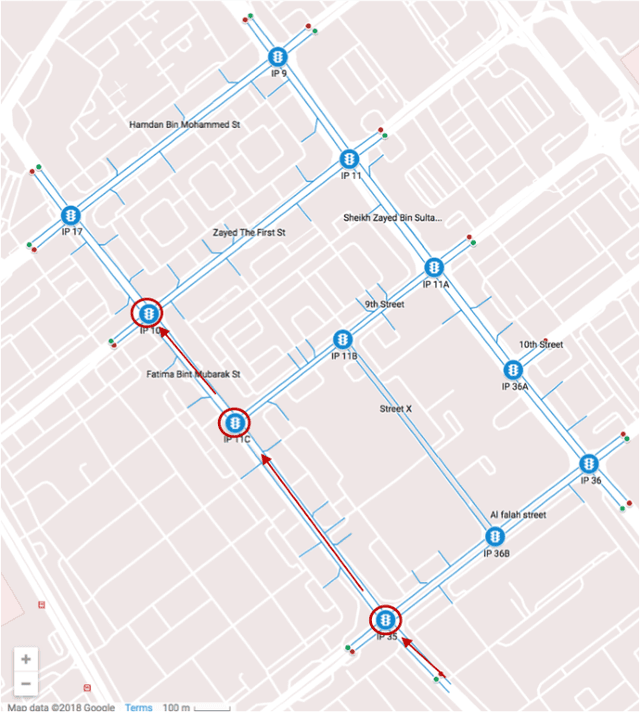
We focus on short-term traffic forecasting for traffic operations management. Specifically, we focus on forecasting traffic network sensor states in high-resolution (second-by-second). Most work on traffic forecasting has focused on predicting aggregated traffic variables, typically over intervals that are no shorter than 5 minutes. The data resolution required for traffic operations is challenging since high-resolution data exhibit heavier oscillations and precise patterns are harder to capture. We propose a (big) data-driven methodology for this purpose. Our contributions can be summarized as offering three major insights: first, we show how the forecasting problem can be modeled as a matrix completion problem. Second, we employ a block-coordinate descent algorithm and demonstrate that the algorithm converges in sub-linear time to a block coordinate-wise optimizer. This allows us to capitalize on the "bigness" of high-resolution data in a computationally feasible way. Third, we develop an adaptive boosting (or ensemble learning) approach to reduce the training error to within any arbitrary error threshold. The latter utilizes past days so that the boosting can be interpreted as capturing periodic patterns in the data. The performance of the proposed method is analyzed theoretically and tested empirically using a real-world high-resolution traffic dataset from Abu Dhabi, UAE. Our experimental results show that the proposed method outperforms other state-of-the-art algorithms.