SUCAG: Stochastic Unbiased Curvature-aided Gradient Method for Distributed Optimization

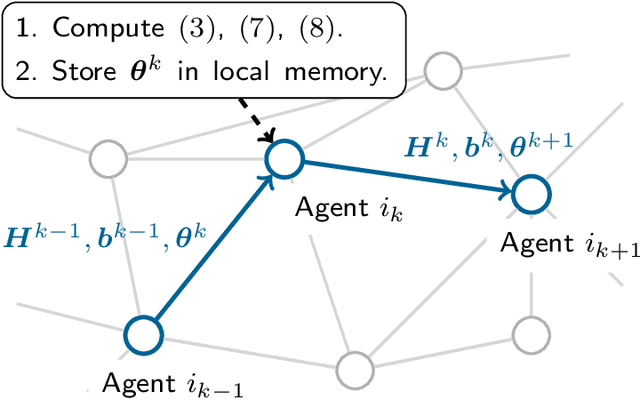
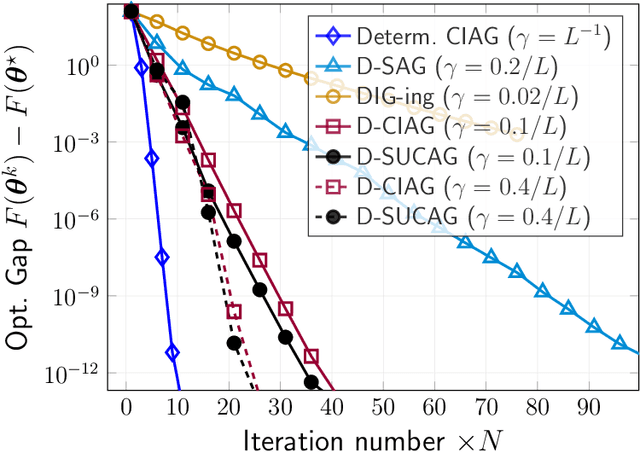
We propose and analyze a new stochastic gradient method, which we call Stochastic Unbiased Curvature-aided Gradient (SUCAG), for finite sum optimization problems. SUCAG constitutes an unbiased total gradient tracking technique that uses Hessian information to accelerate con- vergence. We analyze our method under the general asynchronous model of computation, in which each function is selected infinitely often with possibly unbounded (but sublinear) delay. For strongly convex problems, we establish linear convergence for the SUCAG method. When the initialization point is sufficiently close to the optimal solution, the established convergence rate is only dependent on the condition number of the problem, making it strictly faster than the known rate for the SAGA method. Furthermore, we describe a Markov-driven approach of implementing the SUCAG method in a distributed asynchronous multi-agent setting, via gossiping along a random walk on an undirected communication graph. We show that our analysis applies as long as the graph is connected and, notably, establishes an asymptotic linear convergence rate that is robust to the graph topology. Numerical results demonstrate the merits of our algorithm over existing methods.

Curvature-aided Incremental Aggregated Gradient Method

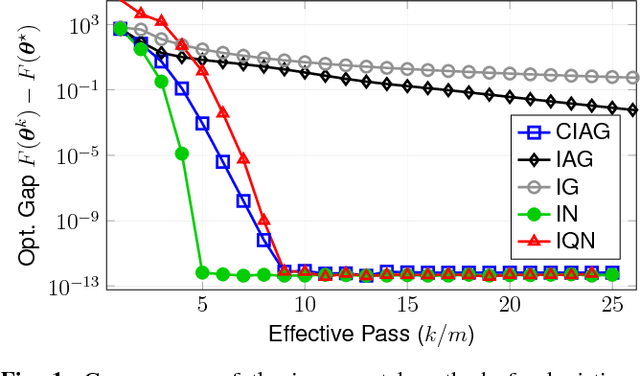
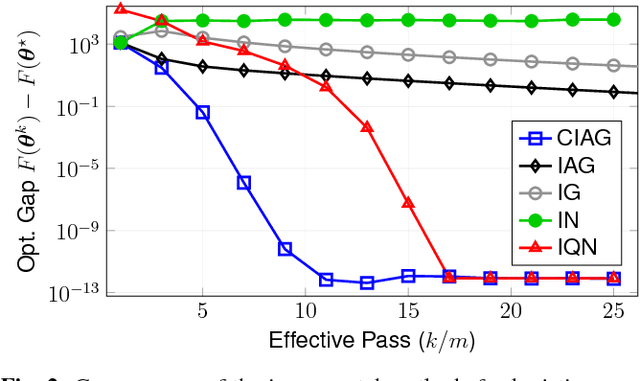
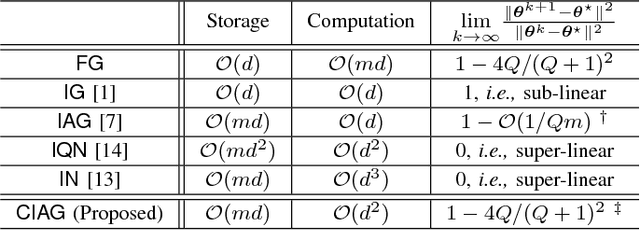
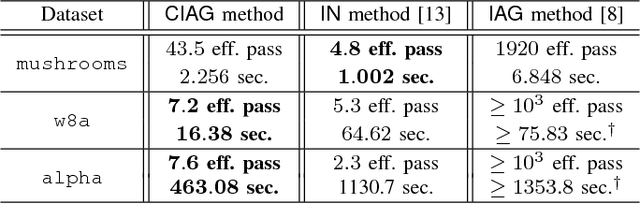
We propose a new algorithm for finite sum optimization which we call the curvature-aided incremental aggregated gradient (CIAG) method. Motivated by the problem of training a classifier for a d-dimensional problem, where the number of training data is $m$ and $m \gg d \gg 1$, the CIAG method seeks to accelerate incremental aggregated gradient (IAG) methods using aids from the curvature (or Hessian) information, while avoiding the evaluation of matrix inverses required by the incremental Newton (IN) method. Specifically, our idea is to exploit the incrementally aggregated Hessian matrix to trace the full gradient vector at every incremental step, therefore achieving an improved linear convergence rate over the state-of-the-art IAG methods. For strongly convex problems, the fast linear convergence rate requires the objective function to be close to quadratic, or the initial point to be close to optimal solution. Importantly, we show that running one iteration of the CIAG method yields the same improvement to the optimality gap as running one iteration of the full gradient method, while the complexity is $O(d^2)$ for CIAG and $O(md)$ for the full gradient. Overall, the CIAG method strikes a balance between the high computation complexity incremental Newton-type methods and the slow IAG method. Our numerical results support the theoretical findings and show that the CIAG method often converges with much fewer iterations than IAG, and requires much shorter running time than IN when the problem dimension is high.

On Projected Stochastic Gradient Descent Algorithm with Weighted Averaging for Least Squares Regression

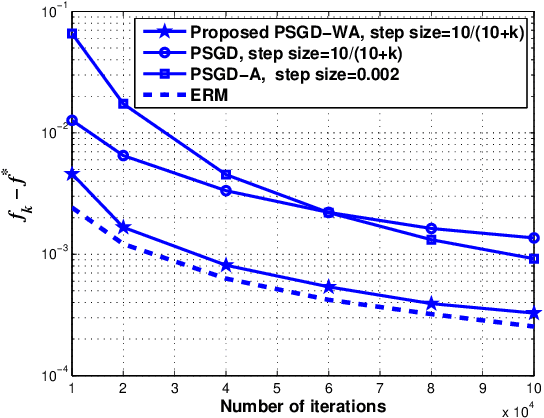
The problem of least squares regression of a $d$-dimensional unknown parameter is considered. A stochastic gradient descent based algorithm with weighted iterate-averaging that uses a single pass over the data is studied and its convergence rate is analyzed. We first consider a bounded constraint set of the unknown parameter. Under some standard regularity assumptions, we provide an explicit $O(1/k)$ upper bound on the convergence rate, depending on the variance (due to the additive noise in the measurements) and the size of the constraint set. We show that the variance term dominates the error and decreases with rate $1/k$, while the term which is related to the size of the constraint set decreases with rate $\log k/k^2$. We then compare the asymptotic ratio $\rho$ between the convergence rate of the proposed scheme and the empirical risk minimizer (ERM) as the number of iterations approaches infinity. We show that $\rho\leq 4$ under some mild conditions for all $d\geq 1$. We further improve the upper bound by showing that $\rho\leq 4/3$ for the case of $d=1$ and unbounded parameter set. Simulation results demonstrate strong performance of the algorithm as compared to existing methods, and coincide with $\rho\leq 4/3$ even for large $d$ in practice.

Data Clustering and Graph Partitioning via Simulated Mixing

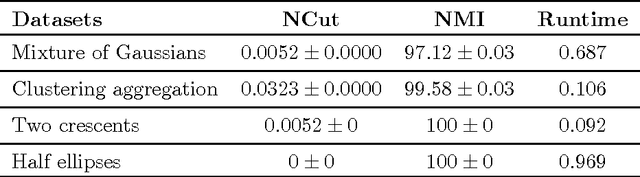
Spectral clustering approaches have led to well-accepted algorithms for finding accurate clusters in a given dataset. However, their application to large-scale datasets has been hindered by computational complexity of eigenvalue decompositions. Several algorithms have been proposed in the recent past to accelerate spectral clustering, however they compromise on the accuracy of the spectral clustering to achieve faster speed. In this paper, we propose a novel spectral clustering algorithm based on a mixing process on a graph. Unlike the existing spectral clustering algorithms, our algorithm does not require computing eigenvectors. Specifically, it finds the equivalent of a linear combination of eigenvectors of the normalized similarity matrix weighted with corresponding eigenvalues. This linear combination is then used to partition the dataset into meaningful clusters. Simulations on real datasets show that partitioning datasets based on such linear combinations of eigenvectors achieves better accuracy than standard spectral clustering methods as the number of clusters increase. Our algorithm can easily be implemented in a distributed setting.