Data Clustering and Graph Partitioning via Simulated Mixing
Paper and Code
Mar 15, 2016
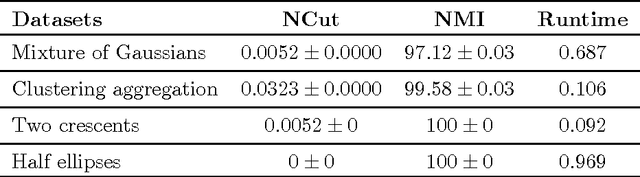


Spectral clustering approaches have led to well-accepted algorithms for finding accurate clusters in a given dataset. However, their application to large-scale datasets has been hindered by computational complexity of eigenvalue decompositions. Several algorithms have been proposed in the recent past to accelerate spectral clustering, however they compromise on the accuracy of the spectral clustering to achieve faster speed. In this paper, we propose a novel spectral clustering algorithm based on a mixing process on a graph. Unlike the existing spectral clustering algorithms, our algorithm does not require computing eigenvectors. Specifically, it finds the equivalent of a linear combination of eigenvectors of the normalized similarity matrix weighted with corresponding eigenvalues. This linear combination is then used to partition the dataset into meaningful clusters. Simulations on real datasets show that partitioning datasets based on such linear combinations of eigenvectors achieves better accuracy than standard spectral clustering methods as the number of clusters increase. Our algorithm can easily be implemented in a distributed setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge